Últimamente los físicos en las redes sociales están muy activos hablando de "la constante Ñu de la mecánica cuántica". El detonante ha sido este artículo de EL PAÍS:
En concreto, el último párrafo dice textualmente:
Como he leído que hay personas que han estudiado la licenciatura o el grado de Física, incluso algunos con un doctorado en Física Cuántica, que afirman no haberse encontrado con esa constante en su vida, he decidido escribir este post para aclarar este importante concepto. Lo que viene a continuación no es un texto fácil, pero merece la pena leerlo despacio y al completo si realmente queremos entender el significado físico de los conceptos de la mecánica cuántica.
Indeterminismo cuántico
En mecánica clásica, la que no es cuántica, los sistemas físicos vienen descritos por una serie de ecuaciones diferenciales, una para cada grado de libertad de cada partícula, del tipo:
Sin embargo, en mecánica cuántica los sistemas físicos no evolucionan según leyes deterministas. Uno de los ejemplos más sencillos se describe en este breve vídeo, que es necesario visionar para poder entender lo que viene a continuación:
Más allá de calcular las probabilidades de los distintos sucesos futuros, es imposible predecir cuál va a ser el resultado de una medición concreta de entre todos los sucesos posibles.
Interferencia entre caminos
Otro característica sorprendente de los sistemas cuánticos es que sufren interferencias:
Pero, para que la suma de todas las probabilidades sea igual a uno, uno en seguida se da cuenta de que lo que tiene que sumar no son las probabilidades asociadas a cada camino, sino las amplitudes de probabilidad. Es decir, la interferencia entre caminos se hace sumando las amplitudes de probabilidad. Este importante concepto se explica en el siguiente vídeo:
Lo más fuerte de todo es que aquí no hay interferencia entre varias partículas, cada una de las cuales ha seguido una trayectoria concreta. Aquí la interferencia es entre cada uno de los caminos asociados a una misma partícula:
Es decir, que en la probabilidad de que una partícula cuántica llegue a un sitio influyen todos los caminos que le llevan a ese sitio, cada uno contribuyendo con una amplitud de probabilidad. No podemos decir que la partícula ha llegado a ese sitio siguiendo ninguno de esos caminos en concreto. Por eso decimos que, en mecánica cuántica, las partículas obedecen al principio de indeterminación. Éste nos dice que, cada partícula, en su movimiento, no sigue una trayectoria bien definida. ¡Ojo! Lo que dice el principio de indeterminación no es sólo que no podemos saber con total precisión cuál es la trayectoria que ha seguido la partícula, sino que la trayectoria, como ente físico, no existe. Usted, querido lector, puede afirmar que su cuerpo ha seguido, desde que se levantó esta mañana de la cama hasta el lugar donde ha tomado el desayuno, una trayectoria bien definida con una precisión de más/menos un micrómetro, pero cada uno de los electrones, protones y neutrones que forman parte de su cuerpo no ha seguido ninguna trayectoria concreta. Y, si no han seguido ninguna trayectoria bien definida, tampoco tienen unos valores de r y v bien definidos simultáneamente (ya que, si estuvieran bien definidos en cada instante de tiempo, entonces la trayectoria también estaría bien definida). Por tanto, lo que ocurre no es sólo que no podemos utilizar las ecuaciones de la mecánica clásica para predecir el futuro, sino que, además, esas ecuaciones de la mecánica clásica no se aplican en este caso. Esas ecuaciones no describen la naturaleza.
Observables mecanocuánticos
Aunque todos los sistemas físicos obedecen al principio de indeterminación, sí es posible seguirle el rastro, seguirle la trayectoria con cierta incertidumbre experimental, a la mayoría de los sistemas macroscópicos. Por ejemplo, es posible ver cómo una aguja de un aparato de medida va pasando de la posición 5 a la posición 6. De esto se aprovecha la mecánica cuántica: los aparatos de medida con los que estudiamos los sistemas físicos son siempre, en buena aproximación, clásicos. Estudiando cómo evoluciona ese sistema clásico mientras interacciona con el sistema cuántico podemos obtener información sobre el sistema cuántico. Este truco nos permite hacer física a pesar del principio de indeterminación. Pero el precio que tenemos que pagar es trabajar con magnitudes físicas que no son características sólo del sistema cuántico, sino que son propiedades del conjunto formado por el sistema cuántico y los aparatos de medida [Landau1962]. Las características dinámicas de los objetos cuánticos sólo están, por tanto, asociadas a los resultados de la medición cuántica, y por eso se les llama "observables". Por ejemplo, si dispongo los aparatos para medir con muchísima precisión la posición de una partícula, el observable "posición" tomará un valor bien definido, pero entonces el observable "velocidad" no tomará una valor bien definido. ¡Ojo! No es que tome un valor bien definido desconocido para nosotros, sino que no toma ningún valor en concreto. Al ser una característica asociada, no sólo al sistema cuántico, sino también a una disposición concreta de los aparatos de medida que hemos decidido no implementar, es una característica de algo que no existe en ese momento y, por tanto, su valor no existe en ese momento. Si, después, ponemos los aparatos de medida de tal forma que midan la velocidad, entonces el observable velocidad sí tomará un valor bien definido, pero no así el observable posición.
Técnicamente, dos magnitudes no pueden tomar nunca valores bien definidos simultáneamente cuando sus correspondientes operadores mecanocuánticos no conmutan. Esto es lo que le ocurre a r y a v. Su conmutador es iħ/m, donde ħ es la constante de Planck dividida entre 2π. El hecho de que en la naturaleza la contante de Planck tome un valor no nulo lo que significa es que r y v no pueden tomar valores bien definidos simultáneamente. Si medimos r con mucha precisión, entonces sí toma un valor bien definido. Pero si no lo hacemos, entonces no tiene por qué. Por eso se dice que la mecánica cuántica no es realista, en el sentido de que trata sobre características dinámicas de los objetos cuánticos que no tienen existencia real más allá del proceso de medición cuántica.
Cuando estaban desarrollando la mecánica cuántica los físicos se dieron cuenta de que para poder comprender la naturaleza era necesario abandonar la costumbre de asignar realidad a aquellos objetos matemáticos, como la trayectoria de una partícula, que no se pueden medir, y trabajar sólo con aquellos objetos que, o bien se pueden medir, o bien su inclusión en la teoría es imprescindible para que haya consistencia con las observaciones. El valor de las magnitudes físicas antes de la medición en la mayoría de las ocasiones no cumple este requisito.
Este punto es necesario aclararlo. El positivismo al que nos ha llevado la mecánica cuántica no nos dice que:
- "Sólo tienen sentido las afirmaciones que sean comprobables experimentalmente o que se deduzcan lógicamente de afirmaciones comprobables experimentalmente."
- "Si algo no se puede definir operacionalmente a partir de los "hechos" de la experiencia, entonces es perfectamente legítimo construir teorías en las que ese algo no tiene significado físico, pero no estamos obligados a ello. Puede ser útil introducir ese algo en la teoría por conssitencia".
No se puede exigir a una teoría, como hacen muchos falsacionistas, que los elementos que no te gustan sean directamente contrastables con la experiencia. Si no es así, eso no es una debilidad de la teoría. La mecánica cuántica dio un paso importante en la eliminación de entes ajenos a la experiencia, pero sigue siendo una teoría científica con sus partes más cercanas y más alejadas de ella.
Probabilidades mecanocuánticas
Nótese que la mecánica cuántica es menos detallada que la mecánica clásica, ya que, por ejemplo, al no tomar r y v valores bien definidos simultáneamente, para determinar el estado cuántico de un sistema hacen falta menos variables dinámicas que en mecánica clásica. Esto implica que las predicciones que hace la mecánica cuántica no pueden ser, aunque se conozca por completo el estado cuántico inicial de un sistema, tan precisas como las de la mecánica clásica. En concreto, todo lo que puede hacer la mecánica cuántica es, dado el resultado de una medida, tratar de predecir, pasado un tiempo t, cuál será el resultado de futura nueva medida. Es decir, la mecánica cuántica sólo nos da probabilidades de que vaya a ocurrir determinado suceso, aunque algunas veces estas probabilidades son del 100%. ¿Cómo pueden calcularse esas probabilidades? Ya lo hemos dicho: sumando las amplitudes de probabilidad de cada camino.
Ya hemos dicho que la mecánica cuántica no es realista. ¿Significa eso que la posición no existe mientras no la midamos? ¿No existe nada mientras no lo midamos? No. La posición bien definida de los protones de mi cuerpo no tiene existencia real en estos momentos. Pero, dado que, ante una hipotética medición, la probabilidad de encontrar a esos protones en el interior de mi despacho es prácticamente del 100%, sí podemos decir que esos protones están en mi despacho. Es un hecho físico sobre el que no tenemos ninguna duda. De hecho, en teoría cuántica de campos, la extensión de la mecánica cuántica para dar cuenta de los fenómenos relativistas, ni siquiera el número de partículas de un sistemas tiene por qué tener un valor bien definido. La mecánica cuántica no niega la realidad, pero sí nos dice que la realidad es muy distinta de lo que ingenuamente esperábamos.
La función de onda
Uno de los conceptos más utilizados y menos entendidos de la mecánica cuántica es el de la función de onda, que es una función que asocia a cada resultado posible una amplitud de probabilidad. Esta amplitud de probabilidad la podemos calcular mediante la suma de caminos de Feynman que hemos explicado anteriormente, o mediante cualquiera de las diferentes técnicas equivalente que los físicos han desarrollado.
Es importante aclarar que la función de onda no es ningún objeto que exista en la naturaleza. Es simplemente una forma conveniente de expresar las amplitudes de probabilidad de cada uno de los posibles resultados. Ante una nueva medición tenemos nueva información, con lo que debemos actualizar la función de onda con esa nueva información. A ese proceso se le denomina "colapso" y, al contrario de lo que algunos estudiantes primerizos piensan, no es un proceso físico que ocurra en la naturaleza, sino un proceso de cálculo que ocurre en la mente del físico.
Simplificando mucho, podemos decir que la función de onda es una forma de representar el estado cuántico en el que se encuentra un sistema. En notación de Dirac, este estado se escribe:
a1|v1>+a2|v2>+a3|v3>+...
Donde a1 es la amplitud de probabilidad de que las magnitudes físicas del sistema cuántico tomen los valores |v1>, a2 es la amplitud de probabilidad de que las magnitudes físicas del sistema cuántico tomen los valores |v2>, etc. Se dice entonces que el sistema cuántico se encuentra en un estado superposición de los estados |v1>, |v2>, |v3>, etc. Por supuesto, si realizamos la medición de esas magnitudes físicas, éstas tomarán sólo uno de los valores posibles. Por ejemplo, tomarán v1 con probabilidad |a1|2.
Un ejemplo concreto: el espín
Por ejemplo, una de las cosas que nos dice la mecánica cuántica es que la mayoría de las partículas tienen un momento angular intrínseco, al que denominamos espín. En el caso de los electrones, que tienen espín s=1/2, el módulo al cuadrado de ese momento angular intrínseco siempre toma el valor
Un truco que no suele venir en los libros de texto es trabajar con los cuadrados de las componentes del momento angular, ya que éstos sí conmutan todos entre sí y, por tanto, sí pueden tomar valores bien definidos simultáneamente. En los estados en los que esto ocurre el vector espín sigue sin tener una dirección bien definida, pero ahora todas sus componentes están bien definidas salvo signo. Los valores que pueden tomar Sx2, Sy2 y Sz2 son 0 y 1. No obstante, como
Supongamos, por ejemplo, que la partícula se encuentra en el estado cuántico:
- el resultado (0, 1, 1) con probabilidad 1/3.
- el resultado (1, 0, 1) con probabilidad 1/3.
- el resultado (1, 1, 0) con probabilidad 1/3.
Veamos otro ejemplo. Si la partícula se encuentra en el estado
- el resultado (0, 1, 1) con probabilidad 1/2.
- el resultado (1, 0, 1) con probabilidad 1/2.
- el resultado (1, 1, 0) con probabilidad 0.
- el resultado (0, 1, 1) con probabilidad 1.
- el resultado (1, 0, 1) con probabilidad 0.
- el resultado (1, 1, 0) con probabilidad 0.
El entrelazamiento cuántico
Uno podría pensar que la afirmación "la mecánica cuántica trata sobre características dinámicas de los objetos cuánticos que no tienen existencia real más allá del proceso de medición cuántica" es sólo una de las interpretaciones posibles de la mecánica cuántica (la que se denomina comúnmente "interpretación de Copenhague") y que hay otras interpretaciones posibles en las que Sx2, Sy2 y Sz2 sí tienen un valores bien definidos antes de la medición. Si esto fuera así, existiría una función definida en la esfera de todas las posibles direcciones del vector espín tal que a cada conjunto de 3 ejes perpendiculares se le asignan los valores 0, 1 y 1 en algún orden, y tal que a direcciones opuestas se les asigna el mismo valor. Se puede demostrar matemáticamente que una función con estas características no existe [Conway2009]. Invitamos al lector a que busque alguna forma coherente de asignar ceros y unos a cada una de las 33 pares de direcciones del siguiente dibujo. No la va a encontrar. Y si no se puede con estas 33 pares de direcciones, menos todavía si admitimos la esfera entera.
Lo que comúnmente se denomina "interpretaciones alternativas de la mecánica cuántica" no son interpretaciones, sino teorías diferentes que predicen resultados experimentales diferentes. ¿Cuáles son esos experimentos en los que la mecánica cuántica y sus alternativas predicen resultados diferentes? Son experimentos en los que el fenómeno del entrelazamiento cuántico juega un papel fundamental. Vamos a ver uno de ellos.
Supongamos una partícula de espín nulo que decae en dos partículas de espín 1 que salen disparadas en direcciones opuestas (con momento angular orbital nulo), una en la dirección en la que está Alice y la otra en la dirección en la que está Bob.
- 0,1,1
- 1,0,1
- 1,1,0
Además de la mecánica cuántica, el otro gran pilar de la física moderna es la teoría de la relatividad. Uno de los postulados de la relatividad especial es el principio de localidad, que nos dice que ningún objeto ni señal puede viajar más rápido que la luz en el vacío. Supongamos que, en el sistema de referencia en el que Alice y Bob están en reposo, ambos realizan sus mediciones simultáneamente.. Como la velocidad de la luz en el vacío es finita, ambos sucesos están completamente desconectados causalmente. Ninguno puede influir causalmente sobre el otro. Una forma de verlo es que existen sistemas de referencia en los que Alice ha medido primero, pero también existen otros sistemas de referencia en los que Bob ha medido primero, y es imposible que una causa sea posterior a su efecto. Esto significa que Alice puede elegir en qué tres direcciones perpendiculares realizar la medición independientemente de qué direcciones haya elegido Bob, y viceversa, suponiendo que ambos disfrutan de libre albedrío. A esta hipótesis, que se deriva de juntar la relatividad especial con la hipótesis del libre albedrío de Alice y Bob, la vamos a llamar MIN.
Supongamos ahora que la mecánica cuántica es más que una teoría incompleta y que, en realidad, los resultados de las mediciones sí estaban escritos con antelación en variables físicas ocultas que no hemos podido medir. Vamos a llamar a esta hipótesis REAL. De acuerdo con ella, en las partículas estaban escritas todas las posibilidades para todas las posibles orientaciones de los ejes que los experimentadores Alice y Bob hayan podido elegir. Eso significa que la respuesta que dé la partícula de Alice a la medición de Sx2, Sy2 y Sz2 va a ser una función, demás de las direcciones concretas que Alice haya elegido, de determinadas propiedades ocultas cuyo valor estaba fijado antes de la producirse la medición. Y lo mismo podemos decir para Bob. Por la ley MIN, la función de Alice no puede depender de las direcciones de Bob y viceversa y, por la ley TWIN, ambas funciones deben dar los mismos valores en el caso de que alguna dirección de Bob coincida con alguna dirección de Alice. Esto quiere decir que debe existir una función que esté definida en toda la esfera de posibles direcciones que sea la que dé los valores a las funciones de Alice y de Bob. Pero hemos visto que no existe ninguna función de estas características que satisfaga además la ley SPIN. Lo que acabamos de hacer, por tanto, es demostrar que REAL, MIN, TWIN y SPIN son incompatibles. Al menos una de estas hipótesis tiene que ser falsa [Conway2009].
El teorema que acabamos de demostrar, publicado por John Conway y Simon Kochen en 2009 como una versión más fuerte de otro publicado con anterioridad, forma parte de un conjunto de teoremas, junto con las famosas desigualdades de Bell, que demuestran que las teorías de variables ocultas son incompatibles con, al menos, alguno de los principios de la mecánica cuántica o de la relatividad especial.
En física quienes mandan son los experimentos. Y en todos los experimentos de entrelazamiento cuántico de este tipo que se han hecho la naturaleza se ha comportado exactamente como predice la mecánica cuántica. Las leyes SPIN y TWIN se cumplen siempre. Por tanto, ante la pregunta de si las leyes de la física son deterministas, sólo tenemos 3 posibles respuestas:
- Opción MC (Mecánica Cuántica): la hipótesis REAL es incorrecta y la mecánica cuántica es correcta. Por tanto, la naturaleza no es realista y las leyes de la física no son deterministas. Las magnitudes físicas no toman ningún valor bien definido antes de la medición. El resultado de la medición no estaba escrito previamente.
- Opción RN (Realista y No Local): la hipótesis incorrecta es MIN porque el principio de localidad no se cumple. La mecánica cuántica es sólo una teoría aproximada. En realidad los resultados de las mediciones sí estaban escritos en variables ocultas. Estaban escritas todas las posibilidades para todas las posibles orientaciones de los ejes que los experimentadores Alice y Bob hayan podido elegir. Pero esto implica que, en el momento de realizar la medición, haya habido una comunicación más rápida que la luz (lo que en algunos sistemas de referencia implica comunicación hacia el pasado) entre las dos partículas para que se puedan poner de acuerdo en dar ambas el mismo resultado. Esto supone abandonar el principio de localidad, que nos dice que nada ni ninguna señal puede viajar más rápido que la luz en el vacío. Es decir, supone asumir que la relatividad especial es incorrecta.
- Opción S (Superdeterminismo): la hipótesis incorrecta es MIN porque Alice y Bob no tienen libertad para elegir las orientaciones que les de la gana. El realismo y la localidad se salvan. Lo que ocurre es que, en realidad, Alice y Bob no son libres a la hora de elegir cómo orientan sus aparatos de medida. Las leyes de la física son deterministas y todo lo que ocurre está determinado por las condiciones iniciales del universo hasta tal punto que Alice y Bob estaban determinados a elegir, y aquí viene lo fuerte, sólo aquellas orientaciones en las que las partículas se comportan como si la mecánica cuántica fuera cierta, pero en realidad no lo es.
Por otro lado, la opción S no merece ni una mínima discusión, por conspiranoica.
El lector interesado en conocer las consecuencias que tiene toda esta discusión en el debate filosófico acerca de si las leyes de la física son o no compatibles con el libre albedrío puede consultar este otro artículo. Damos aquí sólo algunas pinceladas. En ciencias experimentales, hay infinitos experimentos posibles y, en cada uno de ellos, hay infinitas magnitudes que se pueden medir y hay infinitas posibilidades de colocación de los aparatos de medida. Por ejemplo, en el experimento del par de partículas de espín 1 mencionado anteriormente, tanto Alice como Bob pueden elegir infinitas orientaciones posibles de su aparato de medida. La mecánica cuántica nos da una distribución de probabilidad sólo si fijamos qué medidas realizamos en un tiempo inicial y qué medidas realizamos en un tiempo final. Si Alice mide Sx2, Sy2 y Sz2 de su partícula y encuentra el resultado (0,1,1) e inmediatamente vuelve a medir pero con el aparato girado 45º en torno al eje Z, entonces la mecánica cuántica nos dice que sólo hay dos resultados posibles, (0,1,1) y (1,0,1) con probabilidad 1/2 cada una.
- Pongamos que sale (1,0,1). Eso es lo que se llama la "elección de Dirac". Sobre ella Alice no tiene ningún control.
- Pero en ciencia siempre se asume que tenemos libertad para diseñar el experimento de la forma que creemos más adecuada para poder hacer a la naturaleza las preguntas que, pensamos, son más pertinentes de acuerdo con alguna teoría o hipótesis previa. Alice puede orientar su aparato como le dé la gana y eso es lo que se conoce como la "elección de Heisenberg". Si hubiera preferido no girar su aparato estaría midiendo las componentes del espín en los mismos ejes que antes y habría obtenido el resultado (0,1,1) con total seguridad, mientras que las componentes del espín giradas 45º no estarían tomando ningún valor bien definido. Análogamente, Bob tiene también la libertad de realizar la elección de Heisenberg que le dé la gana.
Como hemos explicado antes, hay mucha divulgación sobre el entrelazamiendo cuántico que induce a confusión. Lo que hace Alice al medir su partícula no afecta a los resultados de la medición que hace Bob sobre la suya. Las probabilidades de los resultados de la medición en la partícula de Bob son independientes de si Alice ha medido o no su partícula y de qué observable ha medido. Los resultados aleatorios de las mediciones de Alice y de Bob son las elecciones de Dirac y están correlacionados porque en el pasado las dos partículas interaccionaron. Pero no se puede decir que una elección de Dirac afecte a la otra. Además, esa correlación solo la ve Bob si Alice le ha mandado la información del resultado de sus mediciones. Sea cual sea el observable que mida Bob, las probabilidades de los resultados de la medición de Bob no se ven afectadas por la elección de Heisenberg que haga Alice. También es importante insistir en que ni Alice ni Bob realizan la elección de Dirac. Lo que sí hacen es la elección de Heisenberg (elegir si medir o no y qué observable medir). Pero la elección de Heisenberg de Alice no afecta a la elección de Heisenberg de Bob ni tampoco a la elección de Dirac de Bob.
Conclusión
La conclusión de todo esto es: ¿dónde aparece aquí la misteriosa constante Ñu de la mecánica cuántica? En ningún sitio. Esa constante no existe. Alguien ha querido reírse de la periodista. Nos seguimos leyendo.
Sobre el autor: Sergio Montañez Naz es doctor en física y profesor de secundaria de la enseñanza pública en la Comunidad de Madrid.
Referencias bibliográficas
- Conway, John H.; Simon Kochen (2009). "The strong free will theorem" (PDF). Notices of the AMS. 56 (2): 226–232.
- Landau, L.D. y Lifshitz, E.M. (1962): Teoría cuántica (no-relativista), Barcelona, Volumen 3 del Curso de Física Teórica (1992).
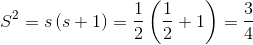
No hay comentarios:
Publicar un comentario