El movimiento más importante en física es el movimiento vibratorio armónico simple (mvas), también conocido como oscilador armónico. La mayor parte de sistemas físicos realizan de manera aproximada este movimiento, desde los átomos que hay en una molécula o en un sólido, que se acercan y se alejan continuamente, pasando por cualquier objeto macroscópico elástico. Hasta el movimiento elíptico de un planeta o de un satélite es en cierta forma un movimiento vibratorio de acercamiento y alejamiento del astro en torno al cual orbita, compuesto con un movimiento de rotación. Es más, las mismas partículas elementales son estados de movimiento vibratorio de una serie de campos cuánticos. El oscilador armónico está en física en todas partes. ¿Por qué? Eso es lo que vamos a ver en este post.
Algebra y geometría de las transformaciones de funciones
Vamos a empezar con una clase de matemáticas. Supongamos que tenemos una función $y=f(x)$ que tiene un máximo en $x=4$ de valor $y=5,5$:
Si multiplicamos esta función por 2, entonces ahora todos los valores de $y$ van a ser el doble de grandes. El máximo estará en en el mismo sitio, pero ahora el valor de ese máximo será el doble de alto. La gráfica de la función va a ser la misma, pero estirada en el eje $y$ hasta el doble de tamaño, sin que haya ningún tipo de deformación en el eje $x$:
Si lo que hacemos, en cambio, es dividir entre 2, entonces todos los valores de $y$ valdrán la mitad. La gráfica se contrae hasta un tamaño la mitad en el eje $y$ sin que haya deformación en el eje $x$:
Pero, ¿qué pasa si multiplicamos por 2, en vez de por fuera, por dentro de la función? La primera respuesta que suelen dar muchos estudiantes de bachillerato es que la gráfica se estira como antes, pero en lugar de en el eje $y$, lo hace en el eje $x$. Sin embargo, la respuesta correcta es justo la contraria. La gráfica no se estira en el eje $x$, se contrae. La regla ahora es AL REVÉS:
Una forma de verlo es pensar en el máximo de la función. Éste estaba en $x=4$ y tomaba un valor $y=f(4)=5,5$. Pero si lo que tenemos ahora es $y=f(2x)$, entonces para poder conseguir ese máximo de valor $f(4)=5,5$ necesitamos que $x$ valga 2, es decir, la mitad. El máximo está ahora a la mitad de distancia de $x=0$ de lo que estaba antes.
Si lo que queremos es expandir la gráfica de la función en un factor 2, lo que hay que hacer es dividir entre dos por dentro de la función:
Algo parecido ocurre con las sumas. Si sumamos a la función el número 2 por fuera, entonces ésta tomará los mismos valores que antes, pero subidos 2 unidades hacia arriba:
O bajados dos unidades si estamos restando:
Pero para que la gráfica se desplace 2 unidades en el eje $x$ en la dirección creciente, lo que hay que hacer no es sumar por dentro, sino restar por dentro. De nuevo, POR DENTRO LA REGLA ES AL REVÉS QUE POR FUERA:
De nuevo, para verlo claramente es mejor fijarse en el máximo. Ahora, para conseguir $f(4)$ necesitamos que $x$ valga 6.
Y si sumamos 2 unidades por dentro, la función se desplaza en el eje $x$ en el sentido negativo:
Si introducimos un signo menos, que es equivalente a multiplicar por $-1$, por fuera la función queda reflejada respecto del eje $x$, ya que todos los valores que toma son los anteriores, pero cambiados de signo.
Y si multiplicamos por $-1$ por dentro, ahora la función se refleja respecto del eje $y$:
ya que para conseguir $f(4)$ necesitamos que $x$ valga $-4$. Aquí la regla también está al revés, pero la transformación de multiplicar por $-1$ es su propia inversa, y por eso parece que es la misma regla.
Representación gráfica de funciones
Las reglas de transformación de funciones que acabamos de ver, junto con el conocimiento de la forma geométrica que adoptan las gráficas de las funciones más sencillas:
nos proporcionan una imagen mental relativamente inmediata de la gráfica de muchas de las funciones que utilizamos. Acabamos de unir álgebra y geometría. A la expresión algebraica de cada función $y=f(x)$ le corresponde una gráfica, una figura geométrica. Ahora nos queda unir el álgebra y la geometría con la física.
El movimiento en un campo conservativo
Una cosa que se puede enseñar a los estudiantes de 1º de Bachillerato es a interpretar la variable dependiente de una función $y=f(x)$ como la energía potencial $E_p=f(x)$ que tiene un objeto situado en un campo conservativo (un campo eléctrico, un campo gravitatorio, etc). Por ejemplo, si, estando un objeto situado en la superficie del planeta Tierra, le damos verticalmente una velocidad muy grande hacia arriba:
E_p=-\frac{GMm}{r}
$$ hay que sumarle la energía cinética que le hemos dado $$
E_c=\frac{1}{2}mv^2
$$ para calcular su energía mecánica. Si la fuerza de rozamiento con el aire es despreciable, esta energía mecánica se conserva, con lo que el objeto se va a mover siguiendo una línea recta en este diagrama, alejándose cada vez más del centro de la Tierra:
A medida que el objeto se aleja del centro de la Tierra, tiene cada vez más energía potencial y menos cinética. Esto significa geométricamente que la hipérbola que nos da la energía potencial se acerca cada vez más a la recta horizontal. En el punto de corte de ambas curvas algebraicamente la energía cinética es igual a cero. Eso significa físicamente que el objeto tiene velocidad nula en ese punto, con lo que cambia de sentido en su movimiento y empieza a caer, esta vez perdiendo energía potencial y ganando cinética. Por este motivo al punto de corte entre la recta horizontal y la hipérbola en este diagrama se le denomina punto de retorno. El objeto no tiene suficiente energía mecánica para llegar más alto.
No obstante, si la suma de energía potencial y energía cinética fuese algebraicamente mayor que cero, entonces geométricamente la recta horizontal y la hipérbola no se cortarían en ningún punto. Esto significa físicamente que no habría punto de retorno. El objeto ascendería eternamente y escaparía del campo gravitatorio terrestre.
Por otro lado, si el objeto, en vez de haber sido lanzado verticalmente hacia arriba, tuviera cierto momento angular $L$ de giro en torno al centro de la Tierra, entonces la gráfica de la energía potencial efectiva tendría una forma ligeramente distinta, ya que hay que añadir el término "centrífugo" $L^2/(2mr^2)$, que es la energía cinética de rotación, pero que ahora podemos considerarla en el paquete de la energía potencial:
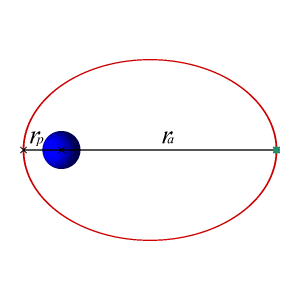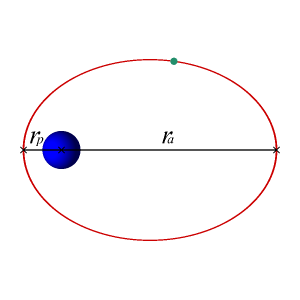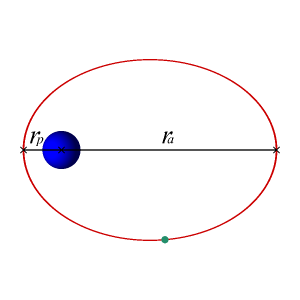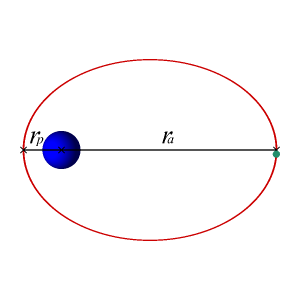
En este caso, cuando la energía mecánica del objeto es menor que cero la recta horizontal corta a la gráfica de energía potencial en dos puntos. Eso significa físicamente que hay dos puntos de retorno: en la dirección radial el objeto oscila entre los puntos de $r$ máximo y mínimo, que se denominan respectivamente $r_a$ (apogeo) y $r_p$ (perigeo), aleándose y acercándose periódicamente del centro de la Tierra. Y, además, hace todo esto mientras gira en torno al centro de la Tierra con momento angular $L$. Se puede demostrar que la trayectoria que seguirá ese objeto es una elipse, con el centro de la Tierra situado en uno de los focos:
Podemos jugar ahora a ver qué le ocurre a la gráfica de la energía potencial cuando multiplicamos $r$, por dentro, por un factor $\alpha$. De acuerdo con las reglas anteriormente vistas, geométricamente esta operación implica "comprimir" la gráfica de energía potencial en el eje horizontal un factor $\alpha$. No obstante, algebraicamente se puede comprobar que la nueva energía potencial es la misma que la que había antes, pero multiplicada por $\alpha^{-1}$, con lo que comprimir la gráfica de la energía potencial en el eje horizontal es equivalente a comprimirla en el eje vertical. $$
E_p(\alpha r)=\alpha^{-1}E_p(r)
$$ (se dice que esta función es una función homogénea de grado $-1$). En cambio, al ser la velocidad la derivada de la posición con respecto del tiempo, ésta quedaría multiplicada por $\alpha$, con lo que la energía cinética quedaría multiplicada por $\alpha^2$, el momento angular $L$ quedaría multiplicado por $\alpha^2$ y el término centrífugo quedaría multiplicado por $\alpha^2$.
Pero si, además, hacemos una transformación similar en la coordenada temporal, entonces, al multiplicar el tiempo $t$ por una constante $\beta$, la velocidad quedaría multiplicada por $\alpha/\beta$, con lo que la energía cinética quedaría multiplicada por $\alpha^2/\beta^2$, el momento angular $L$ quedaría multiplicado por $\alpha^2/\beta$ y el término centrífugo quedaría multiplicado por $\alpha^2/\beta^2$. Si ahora hacemos que $\beta^2=\alpha^3$, obtenemos que todos los términos de la energía mecánica (el término cinético, el potencial y el centrífugo) cambiarían de acuerdo con el mismo factor ($\alpha^-1$). Lo que hemos hecho ha sido escalar el problema. Ahora tenemos exactamente las mismas soluciones para el movimiento del objeto que antes, pero con las distancias multiplicadas por un factor $\alpha$, los tiempos multiplicados por un factor $\alpha^{(3/2)}$ y las energías por $\alpha^{-1}$. Es decir, por cada trayectoria en un objeto en un campo gravitatorio puede haber otros objetos que sigan las correspondientes trayectorias dilatadas.
¿De qué nos ha servido jugar algebraicamente y geométricamente con con estas transformaciones de dilatación del espacio y del tiempo? Acabamos de demostrar la 3º ley de Kepler: los tiempos característicos al cuadrado de cualquier objeto moviéndose en el campo gravitatorio son proporcionales a los cubos de las distancias características. Nótese que estas dilataciones en el tiempo y el espacio funcionan en este problema físico sólo porque la hipérbola $E_p(r)$ es una función homogénea de grado $-1$. Como la pendiente de esta hipérbola es la fuerza gravitatoria (cambiada de signo), esta propiedad es equivalente a que la fuerza gravitatoria es inversamente proporcional al cuadrado de la distancia. Por eso Newton sabía que en la ley de gravitación universal tenía que haber un cuadrado. Si no lo hubiese, no se cumpliría la 3º ley de Kepler. Hoy sabemos que la potencia tiene que ser 2 por un motivo más profundo: vivimos en un universo de 3 dimensiones espaciales (o, mejor dicho, en el que hay 3 dimensiones que no están ocultas, como veremos más adelante, ya que a distancias microscópicas el exponente de la ley de gravitación universal podría ser mayor que 2).
Equilibrios estables e inestables
Como acabamos de decir, la pendiente en toda gráfica de energía potencial $E_p=f(x)$, que algebraicamente es la derivada, se corresponde físicamente con la fuerza conservativa (cambiada de signo) que actúa sobre el objeto en ese campo. $$
F_x=-\frac{dE_p}{dx}
$$ Si el objeto está situado en el mínimo (o en un máximo) de energía potencial, entonces la fuerza conservativa que actúa sobre él es nula (al ser la pendiente nula en ese punto) y por eso ese mínimo es un punto de equilibrio. En cambio, si está ligeramente desplazado del punto de equilibrio, entonces actuará sobre él una fuerza conservativa que, por el signo menos de la fórmula anterior, empujará al objeto en sentido contrario a la pendiente. Si ese punto de equilibrio era un máximo, entonces la fuerza conservativa empujará al objeto en el sentido de alejarlo aún más del punto de equilibrio y se dice que ese punto de equilibrio era inestable.
En cambio, si ese punto de equilibrio era un mínimo, la fuerza conservativa empujará al objeto en el sentido de llevarlo de nuevo al punto de equilibrio y se dice entonces que ese punto de equilibrio es estable.
El objeto oscilará entre dos puntos de retorno en torno a ese punto de equilibrio estable, como hemos explicado antes.
Puedes ver como se va convirtiendo la energía cinética en potencial y viceversa con esta animación creada por Enrique García de Bustos.
Física, álgebra y geometría del oscilador armónico
Cuando la oscilación es pequeña en torno al mínimo de energía potencial, podemos aproximar la gráfica $E_p=f(x)$ por una parábola y se dice entonces que esa oscilación es armónica:
Esto se corresponde algebraicamente con hacer el desarrollo de Taylor en serie de potencias de $x$ (renombrando el origen de $x$ en precisamente ese mínimo) y truncándolo en orden 2. Estamos, por tanto, aproximando la función $f(x)$ por un polinomio de segundo grado que, poniendo el cero en la energía potencial en ese mínimo, es simplemente $$
E_p=0+0\cdot x+ \frac{1}{2}Kx^2,
$$ ya que la primera derivada en el mínimo es nula.
Derivando la función energía potencial para el caso de oscilaciones pequeñas, se obtiene la ley de Hooke $$
F_x=-Kx
$$ Al parámetro $K$ se le denomina constante elástica del problema. El objetivo de toda esta discusión es mentalizar al lector de que los estudiantes de bachillerato sólo entenderán las oscilaciones armónicas en profundidad si son capaces de comprender el triple significado de $K$:
- algebraicamente, es la constante de proporcionalidad en la ley de Hooke, y también la segunda derivada de la función $E_p=f(x)$ en ese mínimo.
- geométricamente, nos dice cómo de cerrada es la parábola que mejor se aproxima a $E_p=f(x)$ en ese mínimo, y también nos da la pendiente de la gráfica de $F_x$ frente a $x$.
- físicamente, no dice cómo de intensa es la fuerza restauradora para un desplazamiento dado respecto del punto de equilibrio estable.
Si esta fuerza conservativa $F_x$ es la única que actúa, entonces, combinando la ley de Hooke con la la segunda ley de Newton $F_x=ma_x$, se obtiene $$
a_x=-\frac{K}{m}x
$$ Como la aceleración $a_x$ es la segunda derivada respecto del tiempo de la función $x(t)$, la función $x(t)$ para el oscilador armónico es tal que su segunda derivada es menos ella misma multiplicada por el factor $$
\omega^2=\frac{K}{m}
$$ Fijando de momento $\omega=1$, vemos que la función $x=\sin (t)$ es solución.
Se observa que, efectivamente, la solución es oscilatoria. El objeto oscila entre los puntos $x=-1$ y $x=1$ con periodo $2\pi$.
Juguemos ahora a transformar esta función con las técnicas que hemos explicado anteriormente, para ver si obtenemos nuevas soluciones.
Por ejemplo, podemos desplazar la gráfica hacia la derecha simplemente restando una cantidad $\delta_o$ por dentro: $$
x=\sin (t-\delta_o)
$$ y la función obtenida sigue siendo solución del problema.
- algebraicamente, lo que se suma a la función por dentro.
- geometrícamente, lo que se desplaza la gráfica en el eje temporal.
- físicamente, el ángulo al que hay que sacarle el seno para hallar la posición inicial del objeto, es decir, en qué fase de la oscilación se encuentra el objeto en $t=0$.
También podemos estirar la gráfica verticalmente, multiplicando por fuera por el parámetro $A$: $$
x=A\sin (t-\delta_o)
$$ y el resultado obtenido sigue siendo solución.
El parámetro $A$ se denomina amplitud, y el triple significado que tiene es:
- algebraicamente, el factor que multiplica a la función por fuera.
- geométricamente, lo que hemos estirado la gráfica verticalmente.
- físicamente, la elongación máxima, es decir, lo máximo que se separa el objeto que oscila de la posición de equilibrio, la distancia de los puntos de retorno al punto de equilibrio.
Si, además, consideramos que el parámetro $\omega$ no es igual a 1, entonces necesitamos que la función también quede multiplicada por $\omega^2$ al derivarla 2 veces. La regla de la cadena nos dice que podemos conseguir esto multiplicando por dentro por $\omega$: $$
x=A\sin (\omega t-\delta_o)
$$ Normalmente, tardo 3 días en explicar esta fórmula a los estudiantes de 1º de Bachillerato: un día para trabajar las transformaciones de funciones (porque en clase de matemáticas eso no suelen hacerlo), otro día para explicar por qué el oscilador armónico es una buena aproximación a cualquier oscilación pequeña, y una tercera para aplicar las dos clases anteriores a la función seno. Así que la eficiencia de este profesor de física es de una fórmula cada 3 días, es decir, 0,33 fórmulas por día. Los burócratas de la educación que quieren estandarizarlo todo considerarían que sería un profesor mucho más eficiente si en 5 minutos escribiera la ecuación del movimiento del oscilador armónico en la pizarra e hiciera memorizar a los estudiantes el nombre de cada una de las letras.
El efecto que tiene al haber multiplicado por dentro por $\omega$ es comprimir la gráfica en el eje temporal, de manera que el periodo de la función ya no es $2\pi$, sino $$
T=\frac{2\pi}{\omega}
$$
El triple significado de $\omega$, que se denomina frecuencia angular, es, por tanto:
- algebraicamente, el factor por el que multiplicamos a la función por dentro.
- geométricamente, el factor con el que comprimimos la gráfica en el eje temporal.
- físicamente, lo rápido que oscila el objeto en torno al punto de equilibrio (la frecuencia de oscilación es $\omega/(2\pi)$).
Para poder entender geométricamente qué significa cada uno de esos parámetros, juega con esta otra simulación creada por Enrique García de Bustos.
Para aprender más sobre por qué el oscilador armónico juega un papel central en toda la física, te recomiendo este vídeo de Ángel Uranga y del equipo de divulgación del Instituto de Física Teórica UAM-CSIC:
El motivo por el que en la naturaleza el oscilador armónico está en todas partes es que los sistemas físicos oscilan en torno a los puntos de equilibrio estables, que son mínimos de energía potencial, y que, cuando esta oscilación es pequeña, la gráfica de la energía potencial en torno a ese mínimo se puede aproximar por una parábola.
Cuanto más cerrada sea esa parábola, mayor será la constante elástica $K$ de ese movimiento vibratorio armónico simple. Cuanto más grande sea $K$, y más pequeña sea la masa $m$, mayor será la frecuencia angular $\omega$ de oscilación. Geométricamente, que $\omega$ sea grande significa que la gráfica espacio-tiempo de ese movimiento está muy comprimida en el eje horizontal, ya que, el hecho de multiplicar por dentro una función, lo que hace es comprimir, no expandir, esa función horizontalmente.
¿Por qué por dentro está al revés? Para entender por qué son necesarias algunas nociones matemáticas que se estudian en el primer curso en la universidad. El lector interesado puede buscarlo en este otro post, que solapa con éste.
Conclusión
El motivo por el que en la naturaleza el oscilador armónico está en todas partes es que los sistemas físicos oscilan en torno a los puntos de equilibrio estables, que son mínimos de energía potencial, y que, cuando esta oscilación es pequeña, la gráfica de la energía potencial en torno a ese mínimo se puede aproximar por una parábola.
Cuanto más cerrada sea esa parábola, mayor será la constante elástica $K$ de ese movimiento vibratorio armónico simple. Cuanto más grande sea $K$, y más pequeña sea la masa $m$, mayor será la frecuencia angular $\omega$ de oscilación. Geométricamente, que $\omega$ sea grande significa que la gráfica espacio-tiempo de ese movimiento está muy comprimida en el eje horizontal, ya que, el hecho de multiplicar por dentro una función, lo que hace es comprimir, no expandir, esa función horizontalmente.
¿Por qué por dentro está al revés? Para entender por qué son necesarias algunas nociones matemáticas que se estudian en el primer curso en la universidad. El lector interesado puede buscarlo en este otro post, que solapa con éste.
Hemos empezando este post con la gráfica de una función:
He enseñado esta gráfica durante años a muchas personas mayores que han estudiado matemáticas y les he preguntado si les daba miedo.
—¿por qué habría de asustar la gráfica de una función? Las matemáticas no me dan miedo. Soy matemática— me responden normalmente.
Pero esta gráfica no es la representación de una función matemática que vive en el mundo de las ideas de Platón. El mundo de los objetos matemáticos no existe. Álgebra, geometría y física son la misma cosa. Este dibujo en realidad representa...
|
|
|
|
|
|
|
V
Sigue bajando
|
|
|
|
|
|
|
V
una serpiente boa que digiere un elefante:
Sobre el autor: Sergio Montañez Naz es doctor en física y profesor de secundaria de la enseñanza pública en la Comunidad de Madrid.

























Gracias por todo el trabajo que publicas y, en particular, por este acercamiento al oscilador armónico simple. No lo había visto nunca. Enhorabuena y gracias.
ResponderEliminarPerdone, pero no entiendo lo que dice el gráfico debajo del video de Ramos. No entiendo el movimiento
ResponderEliminarEs una gráfica que representa la energía potencial en función de la posición. Si a la potencial le sumas la cinética, tienes la energía mecánica.
EliminarUn cordial saludo. Resulta explicito que "en base a la Ecuación Cuántica de Schrodinger resulta que la llamada Constante de Elasticidad K es VARIABLE! (ya que un mismo Oscilador Cuántico puede oscilar a diferentes valores de Frecuencia)". Entonces la pregunta que se impone es: "que fenómeno o componente físico real es el responsable de provocar la variaciin de K?!". Atentamente, José Alberto
ResponderEliminar