"[...] de esta manera tomaría lo mejor del análisis geométrico y del algebra y corregiría los defectos del uno por medio de la otra. Y, en efecto, me atrevo a decir que la exacta observación de los pocos preceptos por mí elegidos me dio tal facilidad para resolver todas las cuestiones de que tratan esas dos ciencias que en dos o tres meses que empleé en examinarlas [...] no solamente resolví muchas cuestiones que en otro tiempo había juzgado muy difíciles, sino que me pareció también, al final, que podía determinar por qué medios y hasta qué punto era posible resolver las que yo ignoraba". Descartes. Discurso del método. Segunda parte.
Tenía motivos Descartes para presumir así. En los años anteriores a escribir estas palabras, y subido a hombros de gigantes como Euclides, Apolonio, Oresme, Viète y Fermat, había conseguido crear un sistema de referencia mediante coordenadas en el plano que le permitió entender los objetos geométicos por medio de expresiones algebraicas. Antes de Descartes y Fermat, la única interpretación geométrica que había de las expresiones algebraicas como $x$, $x^2$ o $x^3$, era, respectivamente, la de una longitud, un área y un volumen. Sin embargo, lo que Descartes y Fermat, más o menos en la misma época y de forma independiente, acababan de crear, era algo mucho más potente: un puente entre geometría y álgebra según el cual los polinomios de primer grado son rectas, los de segundo grado curvas cónicas y los de tercer grado curvas cúbicas [Gonzalez2003]. En palabras de Lagrange, "Mientras el Álgebra y la Geometría han estado separadas, su progreso ha sido lento y sus aplicaciones limitadas; pero cuando estas dos ciencias han sido vinculadas, se han prestado su fuerza mutuamente y han caminado juntas hacia la perfección".
En este post vamos a ver con algunos ejemplos sencillos por qué el establecimiento de este puente entre álgebra y geometría ha constituido uno de los hitos más importantes en la historia de la humanidad. Y vamos a descubrir que las matemáticas no sólo tienen dos caras: álgebra y geometría, sino que hay una tercera cara que, desgraciadamente, se suele ignorar sistemáticamente en las clases de matemáticas que se dan tanto en secundaria como en la universidad.
Algebra y geometría de las transformaciones de funciones
Supongamos que tenemos una función $y=f(x)$ que tiene un máximo en $x=4$ de valor $y=5,5$:
Si multiplicamos esta función por 2, entonces ahora todos los valores de $y$ van a ser el doble de grandes. El máximo estará en en el mismo sitio, pero ahora el valor de ese máximo será el doble de alto. La gráfica de la función va a ser la misma, pero estirada en el eje $y$ hasta el doble de tamaño, sin que haya ningún tipo de deformación en el eje $x$:
Si lo que hacemos, en cambio, es dividir entre 2, entonces todos los valores de $y$ valdrán la mitad. La gráfica se contrae hasta un tamaño la mitad en el eje $y$ sin que haya deformación en el eje $x$:
Pero, ¿qué pasa si multiplicamos por 2, en vez de por fuera, por dentro de la función? La primera respuesta que suelen dar muchos estudiantes de bachillerato es que la gráfica se estira como antes, pero en lugar de en el eje $y$, lo hace en el eje $x$. Sin embargo, la respuesta correcta es justo la contraria. La gráfica no se estira en el eje $x$, se contrae. La regla ahora es AL REVÉS:
Una forma de verlo es pensar en el máximo de la función. Éste estaba en $x=4$ y tomaba un valor $y=f(4)=5,5$. Pero si lo que tenemos ahora es $y=f(2x)$, entonces para poder conseguir ese máximo de valor $f(4)=5,5$ necesitamos que $x$ valga 2, es decir, la mitad. El máximo está ahora a la mitad de distancia de $x=0$ de lo que estaba antes.
Si lo que queremos es expandir la gráfica de la función en un factor 2, lo que hay que hacer es dividir entre dos por dentro de la función:
Algo parecido ocurre con las sumas. Si sumamos a la función el número 2 por fuera, entonces ésta tomará los mismos valores que antes, pero subidos 2 unidades hacia arriba:
O bajados dos unidades si estamos restando:
Pero para que la gráfica se desplace 2 unidades en el eje $x$ en la dirección creciente, lo que hay que hacer no es sumar por dentro, sino restar por dentro. De nuevo, POR DENTRO LA REGLA ES AL REVÉS QUE POR FUERA:
De nuevo, para verlo claramente es mejor fijarse en el máximo. Ahora, para conseguir $f(4)$ necesitamos que $x$ valga 6.
Y si sumamos 2 unidades por dentro, la función se desplaza en el eje $x$ en el sentido negativo:
Si introducimos un signo menos, que es equivalente a multiplicar por $-1$, por fuera la función queda reflejada respecto del eje $x$, ya que todos los valores que toma son los anteriores, pero cambiados de signo.
Y si multiplicamos por $-1$ por dentro, ahora la función se refleja respecto del eje $y$:
ya que para conseguir $f(4)$ necesitamos que $x$ valga $-4$. Aquí la regla también está al revés, pero la transformación de multiplicar por $-1$ es su propia inversa, y por eso parece que es la misma regla.
La geometría analítica
Las reglas de transformación de funciones que acabamos de ver, junto con el conocimiento de la forma geométrica que adoptan las gráficas de las funciones más sencillas:
nos proporcionan una imagen mental relativamente inmediata de la gráfica de muchas de las funciones que utilizamos.
Y, más apasionante aún, ¡esto nos permiten visualizar cuántas soluciones tiene un sistema de ecuaciones dado y cuáles son! ¿Por qué es esto así? Porque los puntos de la gráfica de la función $f(x)$ son aquellos que cumplen una propiedad (que $y=f(x)$). Como escribió D'Alembert, "Descartes es el primero que haya pensado en expresar las líneas curvas por medio de ecuaciones. Esta idea sobre la que se funda la aplicación del Álgebra a la Geometría ha sido muy feliz y fecunda. Está claro que al resolver la ecuación de una curva se obtiene uno o varios valores de la ordenada $y$ para una misma abscisa $x$, y que, en consecuencia, una curva trazada no es otra cosa que la solución geométrica de un problema indeterminado, es decir, que tiene una infinidad de soluciones: es lo que los antiguos llamaban lugar geométrico. Así pues, aunque ellos no pudieron tener la idea de expresar las curvas por medio de ecuaciones, habían visto, sin embargo, que las curvas geométricas no eran otra cosa que el lugar, es decir la sucesión de una infinidad de puntos que satisfacían a la misma cuestión. Por ejemplo, que el círculo era el lugar de todos los puntos que describen los vértices de los ángulos rectos que se pueden formar sobre una misma base dada tomada como diámetro del círculo, y así para las demás curvas."
Buscar la solución al sistema de ecuaciones $$
y=f(x)
$$ $$
y=g(x)
$$ es, por tanto, equivalente a buscar aquellos puntos que satisfagan simultáneamente ambas propiedades, es decir, ¡aquellos puntos en los que las dos gráficas se cortan!
En el ejemplo más sencillo, aplicando estas reglas a la función identidad $y=x$ (la bisectriz), se obtiene inmediatamente la gráfica de cualquier polinomio de grado 1:
Es muy importante que los estudiantes de ESO, cuando estudian la ecuación de la recta $y=mx+n$, aprendan a entender tanto el significado algebraico como el geométrico de cada uno de los elementos de esta ecuación. Por ejemplo, el coeficiente $n$ es:
- algebraicamente, el coeficiente que no va multiplicado por $x$ en la ecuación o, en el lenguaje de las transformaciones que hemos descrito antes, el número que le sumamos a la función por fuera.
- geométricamente, la "altura" $y$ a la que la recta corta al eje vertical (la ordenada en el origen), la distancia que hemos levantado verticalmente la función.
- algebraicamente, el coeficiente que multiplica a $x$, la cantidad con la que hemos multiplicado a la función por dentro.
- geométricamente, la pendiente de la recta, el factor con el que hemos comprimido la gráfica de la recta en el eje horizontal.
Si hacemos sistemas de ecuaciones con estos polinomios de primer grado, los estudiantes de 3º de ESO pueden saber qué soluciones hay y cuánto valen de forma intuitiva simplemente pintando las correspondientes rectas en su mente o en el papel,
y viendo dónde se cortan.
Cuando los estudiantes aprenden a hacer esto, de pronto la tarea de averiguar cuántas soluciones tiene un sistema de ecuaciones se vuelve una tarea mucho más sencilla, a veces casi inmediata.
Por ejemplo, podemos aplicar este método para comprobar que la identidad de Jacobi $$
\vec{a} \times ( \vec{b} \times \vec{c}) + \vec{c} \times ( \vec{a} \times \vec{b}) + \vec{b} \times ( \vec{c} \times \vec{a})=\vec{0}
$$ es equivalente al teorema geométrico que afirma que las tres alturas de todo triángulo se cruzan en un mismo punto:
Es una pena que los libros de matemáticas de bachillerato no suelan enseñar esta relación entre el álgebra de los vectores en tres dimensiones y la geometría euclídea. El lector puede encontrar una demostración de esta equivalencia en este enlace.
Con los sencillos ejemplos que acabamos de mencionar, está claro que esta conexión entre álgebra y geometría, que se estableció al dotar de coordenadas al plano, nos permite asignar un nuevo significado a problemas como establecer relaciones entre vectores, la resolución de ecuaciones y sistemas de ecuaciones o encontrar posiciones relativas, entre otros. Una vez somos capaces de ver ese doble significado, tenemos en nuestras manos poder reformular problemas en geometría como problemas equivalentes en álgebra, y viceversa. Los métodos de cualquiera de las dos áreas se pueden usar para resolver problemas en la otra. Este es el motivo por el que, desde el siglo XVII, la geometría sintética construida por Euclides dejó de ser la protagonista en el quehacer científico, dando paso a la recién nacida geometría analítica.
Tuve una compañera (matemática), que solía decir que "el álgebra es ciega", pero "la geometría es manca". Considerarlas por separado, como ocurría antes de Descartes, nos limita mucho las cosas que podemos hacer. Sin embargo, juntas, parecen no tener límite. ¿Verdad?
La realidad es que abordar los problemas matemáticos combinando ambos puntos de vista, el algebraico y el geométrico, aunque nos permite eliminar muchas limitaciones, no nos libra de todas. Por ejemplo, puede ocurrir que delante de ti se esté cometiendo acoso y discriminación contra otras persona por motivo de su orientación sexual o su ideología y que, si eres ciega, ni siquiera te des cuenta. También puede ocurrir que, no siendo ciega, no hagas nada para evitar esa injusticia por ser manca, por estar atada de pies y manos en esa situación. Pero no ser ni ciega ni manca no garantiza que vayas a hacer algo para evitar esos acosos y discriminaciones, porque puede ocurrir que seas una persona tan intolerante como los que cometen esos abusos y que acabes incluso participando en ellos. Análogamente, la matemática, con este puente entre álgebra y geometría, puede no ser suficiente para resolver muchos problemas. Hace falta un tercer elemento. ¿Eres capaz de ver ya cuál es?
El triple significado de las ecuaciones de movimiento
Si asignamos a la variable independiente $x$ el significado físico de ser el instante de tiempo $t$ en el que ocurren los sucesos, y consideramos que la variable dependiente $y$ es en realidad la coordenada espacial $x$ en la que ocurren estos sucesos, entonces toda función continua $y=f(x)$, que ahora se escribe $x=f(t)$, se puede interpretar como la función que nos da la posición de un objeto que realiza un movimiento rectilíneo en cada instante de tiempo. Es decir, la ecuación $x=f(t)$ es la ecuación de movimiento de ese objeto. Esta idea no es ni mucho menos posterior a Descartes, sino que fue introducida por Nicole Oresme en el siglo XIV.
- Algebraicamente, que una función sea continua significa que el límite de la función en cualquier punto coincide con el valor de la función en ese punto.
- Geométricamente, que se pueda dibujar su gráfica sin levantar el lápiz del papel.
- Y físicamente, que el objeto no pueda desaparecer de donde está e, instantáneamente, aparecer en otro punto del espacio.
Si el movimiento rectilíneo se produce físicamente a velocidad constante (Movimiento rectilíneo uniforme, MRU), entonces la gráfica espacio-tiempo correspondiente es geométricamente una línea recta, es decir la función $f(t)$ es algebraicamente un polinomio de primer grado.
Es muy importante que los estudiantes de ESO, cuando estudian la ecuación de la recta $x=vt+x_o$, aprendan a entender, además del significado algebraico y geométrico de cada uno de los elementos de esta ecuación, también el significado físico. El coeficiente $x_o$ es:
- algebraicamente, el coeficiente que no va multiplicado por $t$ en la ecuación o, en el lenguaje de las transformaciones que hemos descrito antes, en número que le sumamos a la función por fuera.
- geométricamente, la "altura" $x$ a la que la recta corta al eje vertical (la ordenada en el origen), la distancia que hemos levantado verticalmente la función.
- físicamente, la posición del objeto en el instante inicial $t=0$.
- algebraicamente, el coeficiente que multiplica a $x$, la cantidad con la que hemos multiplicado a la función por dentro.
- geométricamente, la pendiente de la recta, el factor con el que hemos comprimido la gráfica de la recta en el eje horizontal.
- físicamente, la velocidad del objeto.
Si la función no es un polinomio de primer grado, geométricamente la pendiente de la gráfica varía. Algebraicamente, eso significa que la derivada de la función es distinta para cada valor de $t$, y físicamente, eso significa que el objeto va cambiando su velocidad a medida que transcurre el tiempo. Si, por ejemplo, la velocidad va variando uniformemente con el tiempo (Movimiento Rectilíneo Uniformemente Acelerado, MRUA), entonces lo que algebraicamente es la segunda derivada, que físicamente es la aceleración $a=f^{\prime\prime}(t)$, es constante. Esto significa geométricamente que la gráfica de $a$ frente a $t$ es una recta horizontal. Entonces, la primera derivada, la velocidad $v=f^\prime(t)$, es algebraicamente un polinomio de primer grado y geométricamente una recta cuya pendiente es $a$ y ordenada en el origen es la velocidad inicial $v_o$. La ecuación de movimiento $x=f(t)$ se obtiene integrando la ecuación de la velocidad, es algebraicamente un polinomio de segundo grado y geométricamente una parábola.
El punto que geométricamente es el vértice de la parábola es algebraicamente el punto donde la derivada se anula, y físicamente el evento espaciotemporal en el que el objeto posee velocidad cero, porque su velocidad está cambiando de sentido. Cuando tenía 14 años, me enseñaron a calcular dónde estaba el vértice de una parábola mediante una fórmula que me tuve que aprender de memoria (ya que todavía no sabía derivar). Me consta que todavía se sigue haciendo en muchas clases de matemáticas en ESO. Hacer eso no me sirvió para nada. Habría aprendido mucho más si me hubieran enseñado el significado físico del vértice de la parábola: el punto de retorno de una piedra que hemos lanzado verticalmente hacia arriba.
Una vez nos hemos mentalizado de que es importante asignar un triple significado a los objetos matemáticos (algebraico, geométrico y físico), vemos que un sistema de ecuaciones no sólo es equivalente a la intersección de curvas, también es equivalente al encuentro de objetos que se mueven.
Tenemos así otra forma intuitiva de visualizar cuántas y cuáles son las soluciones del sistema de ecuaciones: los cruces entre móviles. Por ejemplo, las soluciones a un sistema de ecuaciones formado por una ecuación de primer grado y otra de segundo grado, que geométricamente corresponden con los puntos de interesección de una recta y una parábola, se puede interpretar físicamente como los cruces de una piedra que ha sido lanzada verticalmente hacia arriba y luego cae, y un cohete que asciende a velocidad constante:
El movimiento en un campo conservativo
Lo siguiente que podemos enseñar a los estudiantes, cuando entran ya en Bachillerato es a interpretar la variable dependiente de una función $y=f(x)$ como la energía potencial $E_p=f(x)$ que tiene un objeto situado en un campo conservativo (un campo eléctrico, un campo gravitatorio, etc). Por ejemplo, si, estando un objeto situado en la superficie del planeta Tierra, le damos verticalmente una velocidad muy grande hacia arriba:
E_p=-\frac{GMm}{r}
$$ hay que sumarle la energía cinética que le hemos dado $$
E_c=\frac{1}{2}mv^2
$$ para calcular su energía mecánica. Si la fuerza de rozamiento con el aire es despreciable, esta energía mecánica se conserva, con lo que el objeto se va a mover siguiendo una línea recta en este diagrama, alejándose cada vez más del centro de la Tierra:
A medida que el objeto se aleja del centro de la Tierra, tiene cada vez más energía potencial y menos cinética. Esto significa geométricamente que la hipérbola que nos da la energía potencial se acerca cada vez más a la recta horizontal. En el punto de corte de ambas curvas algebraicamente la energía cinética es igual a cero. Eso significa físicamente que el objeto tiene velocidad nula en ese punto, con lo que cambia de sentido en su movimiento y empieza a caer, esta vez perdiendo energía potencial y ganando cinética. Por este motivo al punto de corte entre la recta horizontal y la hipérbola en este diagrama se le denomina punto de retorno. El objeto no tiene suficiente energía mecánica para llegar más alto.
No obstante, si la suma de energía potencial y energía cinética fuese algebraicamente mayor que cero, entonces geométricamente la recta horizontal y la hipérbola no se cortarían en ningún punto. Esto significa físicamente que no habría punto de retorno. El objeto ascendería eternamente y escaparía del campo gravitatorio terrestre.
Por otro lado, si el objeto, en vez de haber sido lanzado verticalmente hacia arriba, tuviera cierto momento angular $L$ de giro en torno al centro de la Tierra, entonces la gráfica de la energía potencial efectiva tendría una forma ligeramente distinta, ya que hay que añadir el término "centrífugo" $L^2/(2mr^2)$, que es la energía cinética de rotación, pero que ahora podemos considerarla en el paquete de la energía potencial:
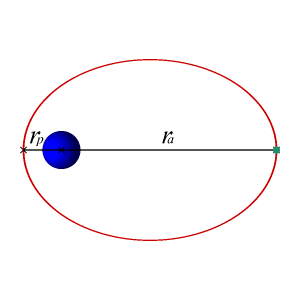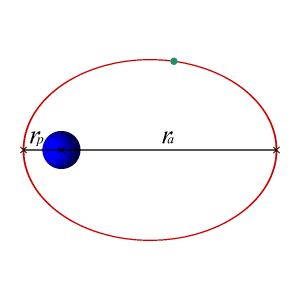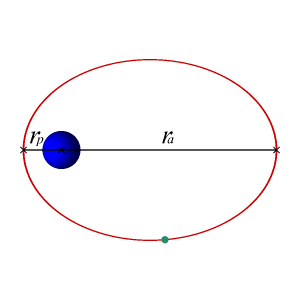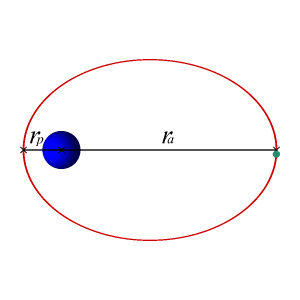
En este caso, cuando la energía mecánica del objeto es menor que cero la recta horizontal corta a la gráfica de energía potencial en dos puntos. Eso significa físicamente que hay dos puntos de retorno: en la dirección radial el objeto oscila entre los puntos de $r$ máximo y mínimo, que se denominan respectivamente $r_a$ (apogeo) y $r_p$ (perigeo), aleándose y acercándose periódicamente del centro de la Tierra. Y, además, hace todo esto mientras gira en torno al centro de la Tierra con momento angular $L$. Se puede demostrar que la trayectoria que seguirá ese objeto es una elipse, con el centro de la Tierra situado en uno de los focos:
Podemos jugar ahora a ver qué le ocurre a la gráfica de la energía potencial cuando multiplicamos $r$, por dentro, por un factor $\alpha$. De acuerdo con las reglas anteriormente vistas, geométricamente esta operación implica "comprimir" la gráfica de energía potencial en el eje horizontal un factor $\alpha$. No obstante, algebraicamente se puede comprobar que la nueva energía potencial es la misma que la que había antes, pero multiplicada por $\alpha^{-1}$, con lo que comprimir la gráfica de la energía potencial en el eje horizontal es equivalente a comprimirla en el eje vertical. $$
E_p(\alpha r)=\alpha^{-1}E_p(r)
$$ (se dice que esta función es una función homogénea de grado $-1$). En cambio, al ser la velocidad la derivada de la posición con respecto del tiempo, ésta quedaría multiplicada por $\alpha$, con lo que la energía cinética quedaría multiplicada por $\alpha^2$, el momento angular $L$ quedaría multiplicado por $\alpha^2$ y el término centrífugo quedaría multiplicado por $\alpha^2$.
Pero si, además, hacemos una transformación similar en la coordenada temporal, entonces, al multiplicar el tiempo $t$ por una constante $\beta$, la velocidad quedaría multiplicada por $\alpha/\beta$, con lo que la energía cinética quedaría multiplicada por $\alpha^2/\beta^2$, el momento angular $L$ quedaría multiplicado por $\alpha^2/\beta$ y el término centrífugo quedaría multiplicado por $\alpha^2/\beta^2$. Si ahora hacemos que $\beta^2=\alpha^3$, obtenemos que todos los términos de la energía mecánica (el término cinético, el potencial y el centrífugo) cambiarían de acuerdo con el mismo factor ($\alpha^-1$). Lo que hemos hecho ha sido escalar el problema. Ahora tenemos exactamente las mismas soluciones para el movimiento del objeto que antes, pero con las distancias multiplicadas por un factor $\alpha$, los tiempos multiplicados por un factor $\alpha^{(3/2)}$ y las energías por $\alpha^{-1}$. Es decir, por cada trayectoria en un objeto en un campo gravitatorio puede haber otros objetos que sigan las correspondientes trayectorias dilatadas.
¿De qué nos ha servido jugar algebraicamente y geométricamente con con estas transformaciones de dilatación del espacio y del tiempo? Acabamos de demostrar la 3º ley de Kepler: los tiempos característicos al cuadrado de cualquier objeto moviéndose en el campo gravitatorio son proporcionales a los cubos de las distancias características. Nótese que estas dilataciones en el tiempo y el espacio funcionan en este problema físico sólo porque la hipérbola $E_p(r)$ es una función homogénea de grado $-1$. Como la pendiente de esta hipérbola es la fuerza gravitatoria (cambiada de signo), esta propiedad es equivalente a que la fuerza gravitatoria es inversamente proporcional al cuadrado de la distancia. Por eso Newton sabía que en la ley de gravitación universal tenía que haber un cuadrado. Si no lo hubiese, no se cumpliría la 3º ley de Kepler. Hoy sabemos que la potencia tiene que ser 2 por un motivo más profundo: vivimos en un universo de 3 dimensiones espaciales (o, mejor dicho, en el que hay 3 dimensiones que no están ocultas, como veremos más adelante, ya que a distancias microscópicas el exponente de la ley de gravitación universal podría ser mayor que 2).
Física, álgebra y geometría del oscilador armónico clásico
Como acabamos de decir, la pendiente en toda gráfica de energía potencial $E_p=f(x)$, que algebraicamente es la derivada, se corresponde físicamente con la fuerza conservativa (cambiada de signo) que actúa sobre el objeto en ese campo. $$
F_x=-\frac{dE_p}{dx}
$$ Si el objeto está situado en el mínimo (o en un máximo) de energía potencial, entonces la fuerza conservativa que actúa sobre él es nula (al ser la pendiente nula en ese punto) y por eso ese mínimo es un punto de equilibrio. En cambio, si está ligeramente desplazado del punto de equilibrio, entonces actuará sobre él una fuerza conservativa que, por el signo menos de la fórmula anterior, empujará al objeto en sentido contrario a la pendiente. Si ese punto de equilibrio era un máximo, entonces la fuerza conservativa empujará al objeto en el sentido de alejarlo aún más del punto de equilibrio y se dice que ese punto de equilibrio era inestable.
En cambio, si ese punto de equilibrio era un mínimo, la fuerza conservativa empujará al objeto en el sentido de llevarlo de nuevo al punto de equilibrio y se dice entonces que ese punto de equilibrio es estable.
El objeto oscilará entre dos puntos de retorno en torno a ese punto de equilibrio estable, como hemos explicado antes.
Cuando la oscilación es pequeña en torno al mínimo de energía potencial, podemos aproximar la gráfica $E_p=f(x)$ por una parábola y se dice entonces que esa oscilación es armónica:
Esto se corresponde algebraicamente con hacer el desarrollo de Taylor en serie de potencias de $x$ (renombrando el origen de $x$ en precisamente ese mínimo) y truncándolo en orden 2. Estamos, por tanto, aproximando la función $f(x)$ por un polinomio de segundo grado que, poniendo el cero en la energía potencial en ese mínimo, es simplemente $$
E_p=0+0\cdot x+ \frac{1}{2}Kx^2,
$$ ya que la primera derivada en el mínimo es nula.
Derivando la función energía potencial para el caso de oscilaciones pequeñas, se obtiene la ley de Hooke $$
F_x=-Kx
$$ Al parámetro $K$ se le denomina constante elástica del problema. El objetivo de toda esta discusión es mentalizar al lector de que los estudiantes de bachillerato sólo entenderán las oscilaciones armónicas en profundidad si son capaces de comprender el triple significado de $K$:
- algebraicamente, es la constante de proporcionalidad en la ley de Hooke, y también la segunda derivada de la función $E_p=f(x)$ en ese mínimo.
- geométricamente, nos dice cómo de cerrada es la parábola que mejor se aproxima a $E_p=f(x)$ en ese mínimo, y también nos da la pendiente de la gráfica de $F_x$ frente a $x$.
- físicamente, no dice cómo de intensa es la fuerza restauradora para un desplazamiento dado respecto del punto de equilibrio estable.
Si esta fuerza conservativa $F_x$ es la única que actúa, entonces, combinando la ley de Hooke con la la segunda ley de Newton $F_x=ma_x$, se obtiene $$
a_x=-\frac{K}{m}x
$$ Como la aceleración $a_x$ es la segunda derivada respecto del tiempo de la función $x(t)$, la función $x(t)$ para el oscilador armónico es tal que su segunda derivada es menos ella misma multiplicada por el factor $$
\omega^2=\frac{K}{m}
$$ Fijando de momento $\omega=1$, vemos que la función $x=\sin (t)$ es solución.
Se observa que, efectivamente, la solución es oscilatoria. El objeto oscila entre los puntos $x=-1$ y $x=1$ con periodo $2\pi$.
Juguemos ahora a transformar esta función con las técnicas que hemos explicado anteriormente, para ver si obtenemos nuevas soluciones.
Por ejemplo, podemos desplazar la gráfica hacia la derecha simplemente restando una cantidad $\delta_o$ por dentro: $$
x=\sin (t-\delta_o)
$$ y la función obtenida sigue siendo solución del problema.
- algebraicamente, lo que se suma a la función por dentro.
- geometrícamente, lo que se desplaza la gráfica en el eje temporal.
- físicamente, el ángulo al que hay que sacarle el seno para hallar la posición inicial del objeto, es decir, en qué fase de la oscilación se encuentra el objeto en $t=0$.
También podemos estirar la gráfica verticalmente, multiplicando por fuera por el parámetro $A$: $$
x=A\sin (t-\delta_o)
$$ y el resultado obtenido sigue siendo solución.
El parámetro $A$ se denomina amplitud, y el triple significado que tiene es:
- algebraicamente, el factor que multiplica a la función por fuera.
- geométricamente, lo que hemos estirado la gráfica verticalmente.
- físicamente, la elongación máxima, es decir, lo máximo que se separa el objeto que oscila de la posición de equilibrio, la distancia de los puntos de retorno al punto de equilibrio.
Si, además, consideramos que el parámetro $\omega$ no es igual a 1, entonces necesitamos que la función también quede multiplicada por $\omega^2$ al derivarla 2 veces. La regla de la cadena nos dice que podemos conseguir esto multiplicando por dentro por $\omega$: $$
x=A\sin (\omega t-\delta_o)
$$ Normalmente, tardo 3 días en explicar esta fórmula a los estudiantes de 1º de Bachillerato: un día para trabajar las transformaciones de funciones (porque en clase de matemáticas eso no suelen hacerlo), otro día para explicar por qué el oscilador armónico es una buena aproximación a cualquier oscilación pequeña, y una tercera para aplicar las dos clases anteriores a la función seno. Así que la eficiencia de este profesor de física es de una fórmula cada 3 días, es decir, 0,33 fórmulas por día. Otros profesores son muchos más eficientes que yo, porque en 5 minutos escriben la ecuación del movimiento del oscilador armónico en la pizarra y hacen memorizar a los estudiantes el nombre de cada una de las letras.
El efecto que tiene hacer esto es comprimir la gráfica en el eje temporal, de manera que el periodo de la función ya no es $2\pi$, sino $$
T=\frac{2\pi}{\omega}
$$
El triple significado de $\omega$, que se denomina frecuencia angular, es, por tanto:
- algebraicamente, el factor por el que multiplicamos a la función por dentro.
- geométricamente, el factor con el que comprimimos la gráfica en el eje temporal.
- físicamente, lo rápido que oscila el objeto en torno al punto de equilibrio (la frecuencia de oscilación es $\omega/(2\pi)$).
La teoría de grupos en la física
Acabamos de ver que, cuando hacemos una transformación algebraica a una función, la regla para ver qué le ocurre geométricamente a su gráfica está al revés cuando hacemos la transformación por dentro que cuando la hacemos por fuera. Así, por ejemplo, cuando multiplicamos por $\omega$ la ecuación de movimiento $x(t)$ del oscilador armónico, pero lo hacemos por dentro (lo que equivale físicamente a multipicar por $\omega$ su frecuencia de oscilación), la gráfica espaciotiempo que describe este movimiento no se estira, sino que se contrae como un acordeón en el eje temporal. La regla de correspondencia entre la expresión algebraica y la geometría está al revés si la transformación se hace por dentro de la función. ¿Hay alguna razón profunda por la cual esto tiene que ser siempre así? Sí, la hay. Para ello tenemos que entender primero el concepto de grupo.
En matemáticas, se denomina grupo a cualquier conjunto con una operación interna que cumpla las propiedades asociativa, la existencia de un elemento neutro y la existencia de un elemento inverso para cualquier elemento. La mejor manera intuitiva de entender qué es un grupo es pensar en un conjunto de transformaciones que se pueden hacer a un sistema físico. La composición de transformaciones es también una transformación y, además, cumple la propiedad asociativa. La transformación inversa de toda transformación es lo que hay que hacer para deshacerla. Y la transformación identidad (no hacer nada) es la que actúa como elemento neutro.
Lo que hace a la teoría de grupos interesante es que los grupos son, en general, no abelianos. Esto significa que el orden en que se llevan a cabo estas transformaciones es importante. Éstas no conmutan en general. Podemos llevar a cabo la transformación $a$, y después la transformación $b$, y el resultado es distinto al que se obtendría si hubiéramos hecho esas dos transformaciones en orden inverso.
Hay grupos de estructura muy complicada y de cualquier número de elementos, hasta infinito no numerable. No obstante, el estudio de muchos grupos se puede simplificar cuando es posible descomponerlo en grupos más pequeños. Esto ocurre cuando el grupo tiene algún subgrupo no trivial con una característica especial, denominado subgrupo normal. En cambio, los grupos que no tienen subgrupos normales no se pueden descomponer en otros y, por tanto, se puede decir que son los bloques constituyentes básicos de la teoría de grupos. Afortunadamente, los matemáticos han sido capaces, en una tarea colectiva que ha durado muchos años, de clasificar los distintos grupos simples que hay, en familias sistemáticas y una colección finita de grupos excepcionales y esporádicos. Dentro de estos grupos esporádicos, el que, de los que tienen un número finito de elementos, es el mayor de todos, se denomina grupo monstruo, y ¡tiene exactamente 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 elementos!
El conjunto de todas las transformaciones que le hemos hecho anteriormente a la coordenada temporal (dilataciones y traslaciones) también tiene la estructura de grupo, aunque en este caso se trata de un grupo continuo con un número infinito no numerable de elementos, ya que el factor de dilatación $\omega$ puede ser cualquier número real positivo, y el desfase $\delta_o$ puede ser cualquier número real. Tras una transformación $a$, la coordenada $t$ se convierte en $\omega_a t + \delta_{oa}$. Si, a continuación, realizamos la transformación $b$, el resultado es $$
\omega_b\omega_a t + \omega_b\delta_{oa}+\delta_{ob},
$$ que no es más que una dilatación temporal mediante un factor $\omega_b\omega_a$ seguida de una traslación temporal mediante una cantidad $ \omega_b\delta_{oa}+\delta_{ob}$. Si, por el contrario, llevamos a cabo primero la transformación $b$ y luego la transformación $a$, el resultado es diferente, y este es el motivo por el que este grupo no es abeliano. La transformación inversa de $a$, que se denota como $a^{-1}$, es una dilatación temporal mediante un factor $\omega_a^{-1}$ seguida de una traslación mediante la cantidad $-\omega_a^{-1}\delta_{oa}$.
Uno de los principios fundamentales de la matemática moderna es que la mejor forma de entender cualquier espacio $E$, dado como conjunto de puntos, es estudiando las funciones que tienen como dominio ese espacio. Así, una forma de estudiar cómo un grupo de transformaciones actúa sobre el conjunto $E$ es mediante la acción de ese grupo sobre el espacio de funciones cuyo dominio es $E$. La ventaja que tiene esto es que las funciones constituyen espacios vectoriales, ya que la combinación lineal de funciones de determinado tipo suele ser también de este tipo. El espacio $E$ puede no ser lineal y tener una estructura geométrica muy complicada, pero el espacio de sus funciones sí lo es. En el ejemplo anterior, el espacio $E$ es la recta real de instantes temporales, parametrizado por la coordenada $t$, y el conjunto de todas las funciones continuas cuyo dominio es $E$ es el espacio vectorial de todos los posibles movimientos rectilíneos. La acción del grupo de dilataciones y traslaciones temporales sobre el espacio de estas funciones se define de la siguiente manera: $$
(a\cdot f)(t)=f(a^{-1}\cdot t).
$$ Esta es la forma matemática rigurosa de expresar la idea de que al dilatar o trasladar la coordenada temporal $t$ por dentro de la función, el efecto que estamos consiguiendo sobre la función es precisamente la dilatación o la traslación inversa. ¿Por qué los matemáticos meten la inversa $a^{-1}$ en esta definición? Lo hacen así para que la acción del grupo sobre las funciones respete la estructura del grupo original. En efecto, si combinamos dos transformaciones: $$
(ba\cdot f)(t)=f((ba)^{-1}\cdot t)=f(\omega_b^{-1}\omega_a^{-1} t- \omega_b^{-1}\omega_a^{-1}\omega_b\delta_{oa}+\delta_{ob})=
$$ $$
=f(a^{-1}\cdot b^{-1}\cdot t)=(a\cdot f)(b^{-1}\cdot t)=(b\cdot (a\cdot f))(t),
$$ se obtiene que la acción de $ba$ actuando sobre las funciones es equivalente a la acción de $a$ sobre ellas, seguida de la acción de $b$. Si no hubiéramos puesto la inversa en la definición, esto no ocurriría.
La abstracción de la idea de estudiar un grupo por su acción sobre las funciones da lugar al concepto de representación. Una representación es una función $R$ que asocia, a cada elemento $a$ de un grupo, su correspondiente transformación en un espacio vectorial, de manera que la estructura del grupo se respete, es decir, que $$
R(b) \cdot R(a)=R(ba)
$$ Es evidente que mapear todos los elementos de un grupo a la transformación identidad en un espacio vectorial es trivialmente una representación. Lo interesante es estudiar las representaciones no triviales de los distintos grupos que reproduzcan la estructura de los mismos de forma fiel. Por ejemplo, es posible representar el grupo monstruo como un conjunto finito de ciertas rotaciones concretas sobre un espacio vectorial. El espacio vectorial de dimensión más pequeña que reproduce la estructura de este grupo de forma fiel tiene 196883 dimensiones. Es recomendable que memorice este número antes de seguir leyendo.
Por ejemplo, al evolucionar temporalmente el sistema físico, las amplitudes de probabilidad de los distintos sucesos mecanocuánticos irán cambiando, pero las probabilidades tienen que seguir sumando uno. Los estados mecanocuánticos irán, por tanto, cambiando según cierta transformación unitaria cuya representación en el espacio de estados llamamos $\hat{U}(t)$. Si llamamos $\psi(t_o)$ a la función de onda del sistema cuántico en un instante $t_o$ dado, el resultado de aplicar el operador evolución $\hat{U}(t)$ a la función de onda es: $$
\psi(t+t_o)=\hat{U}(t) \psi(t_o)
$$ Por otro lado, el desarrollo de Taylor de la función $\psi(t+t_o)$ en torno a $t=0$ es$$
\psi(t+t_o)=\sum_{n=0}^\infty \frac{1}{n!}\frac{d^{(n)}\psi}{dt}(t_o)t^n=e^{t\frac{d}{dt_o}}\psi(t_o)
$$ coincide con el de la función exponencial si aceptamos que pueda haber un operador derivada en el exponente. La conclusión es que el operador evolución en mecánica cuántica se puede escribir como una exponencial de un operador hermítico $$
\hat{U}(t)=e^{-\frac{i}{\hbar}\hat{H}t}
$$ donde a $\hat{H}=i\hbar\frac{d}{dt_o}$ se le denomina operador hamiltoniano del sistema. Matemáticamente, el operador hamiltoniano es un vector perteneciente al álgebra de Lie correspondiente a la representación del grupo de traslaciones temporales sobre el espacio vectorial de estados cuánticos del sistema, es decir, el generador de esas traslaciones temporales en esa representación. En mecánica cuántica, los generadores de transformaciones unitarias son operadores hermíticos que representan físicamente a los observables. En este caso, el observable que representa el hamiltoniano es la energía. Los autovalores de este operador son, por tanto, los posibles valores de la energía del sistema. Por ejemplo, el oscilador armónico cuánticamente sólo puede tener unos valores discretos de la energía, de valores $E_n=\hbar\omega(n+1/2)$, donde $n$ es una número natural (comenzando en cero).
Si el hamiltoniano de un sistema es independiente del tiempo, entonces los autovectores del hamiltoniano, al serlo también del operador evolución, sólo cambian ante una evolución temporal con un factor de fase $$
e^{-\frac{i}{\hbar}Et}=\cos(Et/\hbar)-i\sin(Et/\hbar),
$$ siendo $E$ el autovalor correspondiente. La dependencia temporal de estos estados, que se denominan estacionarios, es la de un oscilador armónico clásico con frecuencia angular $\omega=E/\hbar$. Al seguir siendo autovectores del hamiltoniano con el mismo autovalor, la energía del sistema sigue siendo la misma. Es una cantidad que se conserva.
Si el sistema cuántico posee la simetría de ser invariante ante todos los elementos de un grupo $G$, entonces los operadores unitarios que representan la acción de $G$ sobre los estados cuánticos conmutan con el operador evolución temporal. Esto hace que los generadores de esas representaciones unitarias, que son operadores hermíticos, también conmuten con el operador evolución y con el hamiltoniano. Las magnitudes físicas que representan estos operadores hermíticos serán, por tanto, también cantidades conservadas. Además, un resultado básico y muy importante de la teoría de representaciones de los grupos (el lema de Schur) nos dice que el hamiltoniano, al conmutar con los operadores que implementan las representaciones unitarias de ese grupo de simetrías, tiene que ser proporcional al operador identidad dentro de cada representación. Esto significa físicamente que todos los estados de una misma representación de ese grupo de simetrías son degenerados, tienen todos la misma energía. Por tanto, cuando un sistema cuántico tiene una simetría, el espacio vectorial de todos los estados que tienen una misma energía va a ser siempre una representación de ese grupo de simetría. Retenga este resultado para lo que viene más adelante. Además, esa representación, por ser unitaria, va a ser siempre una suma directa de representaciones irreducibles del grupo $G$.
Hay otro motivo por el que la exponencial del hamiltoniano juega un papel muy importante en física. Si el sistema físico tiene una temperatura finita $T$, entonces la probabilidad de que el sistema físico se encuentre en un estado de energía $H$ tiene que ser proporcional al factor de Boltzmann $$
e^{-H/T}.
$$ Es decir, esta probabilidad será menor cuanto mayor sea la energía del estado y este efecto será más exagerado cuanto menor sea la temperatura. Pensemos, por ejemplo, en un gas. Cada una de las moléculas del gas recibe colisiones al azar por las demás moléculas que le transmiten cantidad de movimiento en todas las direcciones. Lo más probable es que esa molécula reciba tantas colisiones por el lado derecho que por el izquierdo, con lo que, de todos los estados, el más probable es el que tiene poca velocidad, poca energía. Para calcular de forma exacta esa probabilidad habría que dividir entre un factor de normalización $$
Z=\sum e^{-H/T},
$$ que no es más que la suma de estas exponenciales para todos los estados y que se denomina función de partición. Así nos aseguramos de que todas las probabilidades sumen 1. Por ejemplo, para el oscilador armónico cuántico hay sólo un estado estacionario en cada nivel de energía, con lo que la función de partición es $$
Z=\sum_{n=0}^\infty 1\cdot e^{-\hbar\omega(n+1/2)/T}=1q+1q^3+1q^5+...=\frac{q}{1-q},
$$ donde $q=e^{-\hbar\omega/(2T)}$. Recuerde para lo que viene a continuación que, si el espacio de estados de energía en el nivel n-ésimo tuviera dimensión $d$, entonces el coeficiente correspondiente en la expansión en serie de potencias de $q$ de la función de partición no sería $1$, sino $d$.
Nótese también que el factor de Boltzmann se puede entender como la continuación analítica del operador evolución temporal, ya que la diferencia entre ambos no es más que in factor $i$ en el exponente. Este truco nos permite a los físicos calcular funciones de partición mediante amplitudes mecanocuánticas.
Los efectos negativos de la separación artificial entre física y matemáticas
Si la física, el álgebra y la geometría son en realidad caras distintas de una misma cosa, ¿por qué entonces en las distintas asignaturas de matemáticas en bachillerato y en la universidad apenas se habla de física? Voy a intentar argumentar que, en realidad, la separación actual, como áreas de conocimiento y de investigación distintas, entre física y matemáticas es más bien un fenómeno social.
En primer lugar, basta estudiar un poco la historia de la física y de las matemáticas para darse cuenta de que hasta comienzos del siglo XX las matemáticas y la física eran la misma disciplina, cultivada por las mismas personas. Es cierto que a principios de ese siglo la comunidad de físicos/matemáticos ya era consciente de la necesidad de construir las matemáticas sobre fundamentos firmes (axiomas y postulados de los que, aplicando una serie de reglas lógicas, se obtengan teoremas) al margen de los principios y las leyes de la física, para evitar así que las matemáticas colapsen cada vez que se descubra algún hecho sorprendente sobre el mundo real. Así, se puede asignar existencia real a las ecuaciones que gobiernan el comportamiento del fluido calórico, al menos como objetos matemáticos en el mundo de las ideas, de forma que toda esa matemática no sea destruida tras descubrir que el fluido calórico no existe. Y lo mismo ocurre con la trayectoria de una partícula puntual. Posee una definición matemática que sigue siendo válida aunque la física cuántica nos haya hecho ver que las trayectorias en realidad no existen en la naturaleza, ya que las partículas puntuales, en su movimiento, no describen ninguna trayectoria bien definida. En el cálculo mecánocuántico de la amplitud de probabilidad de que la partícula acabe en un sitio concreto intervienen simultáneamente todas las trayectorias, sobre todo aquellas que no son diferenciables.
Sin embargo, el trabajo que realizan los matemáticos de construcción de su disciplina sobre fundamentos firmes no difiere en cuando a cualidad del que realizan los físicos teóricos. Después de todo, para que podamos confiar en los teoremas de las matemáticas los sistemas axiomáticos a los pertenecen han de ser consistentes, y el segundo teorema de Gödel nos dice que dentro de un mismo sistema axiomático no es posible probar su consistencia. Por tanto, la consistencia de las matemáticas modernas es más una hipótesis con un fuerte apoyo experimental, como las de la física mejor establecida, que una verdad a priori, sólo que con un apoyo cuantitativamente más fuerte. Además, la mayoría de los problemas y los resultados en matemáticas siguen estando relacionados, directa o indirectamente, con el mundo real, y las intuiciones aprendidas del estudio del mundo real siguen ayudando mucho a los matemáticos, aunque no siempre lo reconozcan.
En segundo lugar, al contrario de lo que nos hacen creer en clase de matemáticas, no es descabellado pensar que en cierto sentido lo que suelen hacer los matemáticos es en realidad más práctico y menos abstracto que lo que hacemos los físicos teóricos. Tanto matemáticos como físicos teóricos definimos objetos, demuestramos teoremas y resolvemos problemas matemáticos. Sin embargo, mientras que los físicos teóricos, cuando encontramos las ecuaciones que gobiernan algún problema profundo que nos interesa, solemos considerar a éste como "resuelto" (ya que el trabajo que queda es, al menos en principio, mecánico), los matemáticos consideran más bien que el grueso de su trabajo es precisamente la búsqueda de esas soluciones y el estudio de las propiedades que poseen. A la vez, los matemáticos suelen despreciar la tarea principal que realizan los físicos teóricos: la búsqueda de las preguntas y los problemas adecuados y la exploración de las implicaciones que tienen las distintas hipótesis en esas cuestiones para ver si se pueden establecer o no como los principios fundamentales que nos delimitan lo que se puede y lo que no se puede hacer. Pero es precisamente esta búsqueda la parte más abstracta y general del quehacer de los físicos/matemáticos. En cambio, resolver problemas predeterminados es una actividad más práctica, más aplicada, menos "teórica".
El enunciado de finales del siglo XIX, que falsamente se atribuye a Lord Kelvin, de que ya no quedaban principios físicos que descubrir, y que lo que quedaba era realizar mediciones cada vez más precisas encaja muy bien en la forma de pensar de muchos matemáticos: resolver problemas utilizando reglas bien establecidas. Pero precisamente la física ha demostrado a lo largo de toda su historia, reciente y no reciente, que reglas del juego que pensábamos bien establecidas, como, por ejemplo, que las partículas en su movimiento describen trayectorias bien definidas, no son adecuadas para describir la naturaleza y tienen que ser sustituidas por otras. Estas reglas no son obvias. Por ejemplo, la geometría de una variedad, tal y como la conciben los matemáticos, está basada en aquellos elementos que una partícula puntual es capaz de explorar al moverse por ese espacio. Pero, ¿qué ocurre si las partículas puntuales no existen, y los objetos fundamentales son extensos, como postula la teoría de cuerdas? Las reglas del juego cambian completamente, como vamos a ver más adelante en este texto. Los matemáticos no pueden ignorar estos cambios en lo que se puede o no se puede hacer, porque precisamente los objetos matemáticos con propiedades más profundas e interesantes son aquellos que son más naturales desde el punto de vista físico.
El problema es que a mediados del siglo XX hubo una serie de matemáticos muy influyentes a los que esta distinción sin frontera clara entre las matemáticas puras y la física teórica no les pareció suficiente. Los que más influencia tuvieron son los que formaron parte del grupo Bourbaki. Este grupo publicó, bajo la excusa de reconstruir toda la matemática de forma mucho más rigurosa, decenas de libros en varios volúmenes con la ideología de que cualquier tipo de significado físico, y muchas veces también geométrico, de los objetos matemáticos debe silenciarse y ocultarse a los jóvenes. El resultado de esta influencia ha sido, usando palabras de Vladímir Ígorevich Arnold, uno de los matemáticos más prolíficos de la historia, que:
"Generaciones completas de matemáticos se formaron sin conocer la mitad de su ciencia y, naturalmente, bajo la total ignorancia de las demás ciencias. Estos matemáticos empezaron primero por enseñar su horrible pseudo-matemática escolástica a sus estudiantes, y después a los niños en los colegios [...]. Como la matemática escolástica que surge de suprimir la física de los temarios no es adecuada ni para la enseñanza ni para su aplicación a las demás ciencias, esto provocó que se extendiera un odio universal hacia las matemáticas, tanto en lo que respecta a los pobres niños de los colegios (algunos de los cuales acaban siendo ministros) como por parte del resto de usuarios.
[...]
Este horrible edificio, construido por matemáticos incultos que no daban para más por su complejo de inferioridad, y que eran incapaces de familiarizarse con la física, [...] predominó en la enseñanza de las matemáticas durante décadas. Habiéndose originado en Francia, esta perversión rápidamente se expandió a la enseñanza de los fundamentos de las matemáticas, primero a los estudiantes universitarios y luego a los colegios y centros de secundaria (primero en Francia, y luego en los demás países, Rusia incluida).
[...]
De acuerdo con mi propia experiencia dando clases en la universidad en Francia, la idea que tienen los estudiantes universitarios acerca de las matemáticas [...] es tan pobre como la de los niños de los colegios. Por ejemplo, estos estudiantes nunca han visto un paraboloide, y preguntas como cuál es la forma de la superficie dada por la ecuación $xy=z^2$ dejan a los estudiantes de la École Normale Supérieure (ENS) en estado de shock. Pintar una cuva en un plano dada mediante ecuaciones paramétricas, como $$
x=t^3-3t
$$ $$
y=t^4-2t^2,
$$es una tarea totalmente imposible para estos estudiantes (y, probablemente, incluso para la mayoría de los profesores de matemáticas). Comenzando por el primer manual de de cálculo de la historia, de l'Hôpital ("cálculo para entender las líneas curvas") y más o menos hasta el manual de Goursat, la habilidad para resolver este tipo de problemas se había considerado siempre [...] como una de las destrezas indispensables que tienen que poseer todo matemático. Pero los fanáticos de las "matemáticas abstractas" suprimieron la geometría (a través de la cual tiene lugar habitualmente en matemáticas la conexión con la física y la realidad) de la enseñanza. Manuales de cálculo como los de Goursat, Hermite, y Picard han sido recientemente desechados por la biblioteca de estudiantes del campus universitario de Jussieu en París por obsoletos y, por tanto, dañinos (fueron sólo rescatados gracias a mi intervención)" [Arnold1998].
Invito al lector a leer el discurso completo de Arnold dado en el Palais de Découverte en Paris en 1997. Da muchos más ejemplos como estos y no tiene desperdicio.
El papel de la física en la matemática de las últimas décadas
Interpretar los objetos y los problemas matemáticos en el contexto de sistemas físicos (reales o imaginarios) ha demostrado ser, no no sólo un ejercicio muy útil para los estudiantes, sino también una herramienta muy potente y fundamental para la investigación de alto nivel en matemáticas. Los ejemplos a lo largo de la historia de grandes avances en las matemáticas que se han llevado a cabo gracias a la intuición física de grandes pensadores son tan numerosos que es imposible recoger aquí siquiera una lista de los más importantes.
Lo que sí quiero remarcar en este texto es que, a pesar del daño causado durante la segunda mitad del siglo XX por intentar aislar a los matemáticos de la física, esta influencia positiva de la física en el desarrollo de las matemáticas se está potenciando de nuevo. Como afirma el actual director del Instituto de Estudios Avanzados de Princeton, Robert Dijkgraaf, "en las últimas décadas las nuevas ideas en teoría cuántica de campos, física de altas energías y teoría de cuerdas han transformado completamente las matemáticas, conduciéndonos a la solución de algunos problemas profundos, sugiriendo nuevos invariantes en geometría y topología y, quizás más importantemente, poniendo a las matemáticas modernas en un contexto natural" [Dijkgraaf2015].
Por ejemplo, las teorías cuánticas de campos topológicas son teorías físicas en las que los valores esperados de los observables mecanocuánticos codifican información sobre la topología de las variedades en las que "viven". Esto le sirvió a Edward Witten para encontrar en 1989 que muchos invariantes topológicos de la teoría de nudos y sus entrelazamientos descubiertos durante los años 80 (como los polinomios HOMFLY, que incluyen a los de Jones, y también como los polinomios de Kaufmann) pueden ser reinterpretados físicamente como funciones de correlación de operadores lazo de Wilson en la teoría de Chern-Simons, que es una teoría gauge en tres dimensiones con invariancia topológica.
Witten también demostró que las funciones de partición de la teoría de Chern-Simons proporcionaban nuevos invariantes topológicos de variedades tridimensionales, y mediante la obtención de la solución exacta a esta teoría pudo establecer una sorprendente conexión entre los nudos y los invariantes de variedades tridimensionales. Por todo este trabajo fue galardonado con la Medalla Fields en 1990. Los matemáticos habían estado siglos intentando clasificar los nudos, pero desde Witten sabemos que los invariantes que los caracterizan no son más que diferencias de fase entre caminos cuánticos que interfieren en la integral de camino de Feynman si interpretamos cada nudo como el camino cerrado que surge de componer uno de los caminos con el inverso del otro camino. Al introducir esto en teoría cuántica de campos, ¡podemos así describir los nudos mediante diagramas de Feynman!
Por otro lado, el estado de la geometría enumerativa ha cambiado radicalmente gracias a la teoría de cuerdas. Por consistencia de la teoría de cuerdas, las supercuerdas viven en 9 dimensiones espaciales y una temporal. Como el universo observado tiene 3 dimensiones espaciales, las otras 6 deben estar ocultas: deben ser compactas y de pequeño tamaño. Podemos dar una interpretación física a las variedades de tipo Calabi-Yau de 3 dimensiones complejas (6 reales) como las dimensiones ocultas en teoría de cuerdas, ya que éstas variedades son soluciones de las ecuaciones de Einstein de la relatividad general. Si hacemos esto, vemos que algunas funciones de correlación de la teoría de cuerdas compactificada en estas variedades Calabi-Yau nos permiten calcular el número de mapas holomorfos que van desde la sábana de mundo bidimensional de la cuerda hasta el espacio target Calabi-Yau y que, por tanto, estas funciones de correlación, que se calculan con integrales de camino de Feynman, contienen información acerca de la geometría enumerativa de estos espacios. Esto condujo a la introducción de los invariantes de Gromov-Witten en matemáticas como una forma de capturar toda esta información. Además, el descubrimiento en estas compactificaciones en teoría de cuerdas de una simetría inesperada, denominada mirror symmetry, permitió a los físicos calcular las funciones generatrices de estos invariantes, lo que les permitió resolver con herramientas físicas problemas enumerativos muy difíciles [Hori2003]. Por ejemplo, los físicos de cuerdas fueron capaces de calcular el número de curvas dadas por ecuaciones paramétricas cúbicas (de grado 3) en el quintic, que es la variedad compacta de tipo Calabi-Yau de 3 dimensiones complejas más simple. Hay 3172016375 curvas de este tipo.
¿Qué truco habían utilizado los físicos? En realidad fueron dos trucos. El primero de ellos es que la teoría de cuerdas es una teoría cuántica que nos permite combinar elegantemente los números de curvas de cualquier grado en una única función que físicamente no es más que una amplitud de probabilidad de la cuerda propagándose por esa variedad Calabi-Yau. Los matemáticos consideraban que se trataba de un problema distinto para cada grado, pero los físicos pudieron abordarlos todos de una sola tacada.
Para entender el segundo truco, es importante volver sobre el hecho de que en teoría de cuerdas los objetos fundamentales no son puntuales, sino que son cuerdas cerradas y abiertas. Y resulta que, por la forma en que interaccionan estos objetos extensos, las cuerdas que se mueven en una de estas direcciones ocultas de pequeño tamaño son equivalentes a las que están enrolladas en otras variedades compactas de tamaño el inverso del tamaño anterior. Hay una simetría perfecta entre los fenómenos físicos de ambas descripciones, con lo que no hay forma de distinguir una situación de otra mediante experimentos: son situaciones físicamente equivalentes:
La mirror symmetry es una generalización de esta simetría que relaciona dos variedades de tipo Calabi-Yau que geométricamente (y también algebraicamente) son muy distintas, pero que físicamente en teoría de cuerdas son equivalentes. Resulta que objetos de geometría algebraica en un Calabi-Yau se corresponden, al aplicar mirror symmetry, con objetos de geometría simpléctica en su Calabi-Yau espejo. En palabras de Nick Sheridan, "la geometría algebraica es un mundo más rígido, mientras que la geometría simpléctica es más flexible. Esta es una de las razones por la que se trata de mundos tan diferentes y es tan sorprendente que hayan resultado ser equivalentes en un sentido profundo". Un cálculo, como la amplitud de probabilidad que nos da el número de curvas que hemos mencionado antes, puede ser muy complicado en un Calabi-Yau, pero reducirse a una simple integral en el otro.
Este es el ejemplo más claro de que no basta con estudiar estas variedades desde el punto de vista geométrico y algebraico. Hizo falta ponerlas también en el contexto de la física para poder llevar a cabo este avance. Ni con las ecuaciones algebraicas ni con su interpretación geométrica podían los matemáticos siquiera imaginarse esta importante relación entre geometría algebraica y geometría simpléctica. Pero al cambiar las reglas del juego, la pregunta de cuál es la geometría del universo ha dejado de tener sentido, ya que ningún experimento es capaz de distinguir entre descripciones duales equivalentes. Para ello necesitaríamos explorar el universo con partículas puntuales, pero éstas podrían resultar ser un mito, como el flogisto, el fluido calórico o el éter luminífero. La concepción clásica de la geometría cambia por completo si todo lo que existe en el universo son objetos extensos. Esta importante lección que nos ha enseñado la teoría de cuerdas no puede ser ignorada por ningún matemático ni ningún físico, por mucho que se nieguen a estudiarla, ya sea por falta de tiempo o por pereza intelectual. Mirror symmetry es en estos momentos uno de los campos más florecientes de las matemáticas.
Y mirror symmetry es sólo un tipo dentro de la gran cantidad de dualidades con las que se trabaja actualmente en física teórica. Por ejemplo, en los últimos 20 años estos dos grandes avances que acabamos de mencionar, el de los nudos con la teoría de Chern-Simons y el de la geometría enumerativa con el sector topológico de la teoría de cuerdas, se han podido conectar gracias a las dualidades de gran N que establecen la equivalencia de teorías gauge con cuerdas cerradas. Una de estas dualidades, la dualidad de Dijkgraaf-Vafa, físicamente no es más que la equivalencia entre la descripción de un estado mecanocuántico mediante una función de onda en la representación coordenadas y una representación basada en estados coherentes estrujados (algo así como tener aparatos de medida que detectan puntos gordos en el espacio de fases). Esto tiene implicaciones profundas que todavía no entendemos bien. Sobre esto trató mi tesis doctoral, así que no hace falta que exprese que todas estas conexiones me parecen apasionantes (¿o a lo mejor no?).
Para ver un último ejemplo de la utilización de conceptos físicos para resolver problemas matemáticos de alto nivel, necesitamos entender qué es el grupo modular. Imaginemos que, en el plano complejo $z=\sigma+it$, tenemos una red de vectores dada por aquellos números complejos cuyas partes reales e imaginarias sean números enteros.
Supongamos que ahora consideramos como equivalentes aquellos puntos del plano complejo que difieran por uno de estos vectores de la red. Lo que se obtiene es, topológicamente hablando, un 2-toro:
Pero éste no es el toro complejo más general que podemos construir. Si utilizamos la red generada por el número complejo $\tau=\tau_1+i\tau_2$ y por la unidad $1$,
Al parámetro complejo $\tau$ se le denomina estructura compleja del 2-toro. Lo interesante aquí es que hay distintos valores de $\tau$ que dan lugar al mismo 2-toro con la misma estructura compleja. Por ejemplo, $\tau$ y $\tau+1$ generan la misma red. Y lo mismo ocurre con $1/\tau$, siempre que reescalemos el tamaño de la cuadrícula para que su altura sea la misma que antes.
El conjunto de todas las transformaciones que podemos hacerle a $\tau$ de forma que sigamos teniendo el mismo toro es un grupo, denominado grupo modular. El conjunto de todas las posibles estructuras complejas distintas de un 2-toro no es por tanto todo el plano complejo (no es el conjunto de todos los valores de $\tau$), sino que es el conjunto de todos los valores de $\tau$ que no son equivalentes entre sí mediante una transformación modular. Por ejemplo, podemos coger como dominio fundamental todos los valores de $\tau$ cuya parte real esté entre $-1/2$ y $+1/2$ y cuyo módulo sea mayor que uno:
Se puede demostrar que la función que mapea este dominio fundamental con la totalidad del plano complejo es única (salvo algunas transformaciones). A esta función se la denomina función j.
En el límite en el que la parte imaginaria de $\tau$ se hace muy grande, la cantidad $q=\exp (2\pi i \tau)$ se hace muy pequeña, y la función j tiene una expansión en serie de potencias de $q$ de la forma $$
j(\tau)=q^{-1}+744+196884q+21493760q^2+...
$$
Como hemos visto antes, el número 196884 es una unidad mayor que la dimensión de la representación más pequeña no trivial del grupo monstruo. Parece una casualidad, pero no lo es, ya que el siguiente coeficiente de la expansión, 21493760, también coincide con otra suma de dimensiones de representaciones irreducibles de este mismo grupo. A esta sorprendente coincidencia entre dos ramas de la matemática aparentemente desconectadas entre sí (la teoría de funciones complejas y las representaciones de grupos finitos esporádicos) se la llamó monstrous moonshine [Conway1979]. De nuevo, utilizando sólo la doble interpretación algebraica y geométrica de estos objetos fue imposible para los matemáticos encontrar la razón por la que estos números coincidían. Fue necesario explorar el significado físico de estos objetos.
Imaginemos un sistema cuántico ligado. Al ser ligado, tendrá niveles de energía discretos. Por tanto, al calcular la función de partición de este sistema, si llamamos $2\pi\tau_2$ al inverso de su temperatura, al sumar para todos los estados tendremos una serie de potencias de $q=\exp(-2\pi\tau_2)$, donde los exponentes de $q$ serán los niveles de energía en determinadas unidades. Si en ese sistema físico hay cosas que oscilan poco, entonces estos niveles de energía serán proporcionales a números enteros. No obstante, como hemos explicado antes, todos aquellos sumandos que correspondan a estados de la misma energía serán iguales, con la misma potencia de $q$, y se pueden sacar factor común. Los coeficientes de esa serie de potencias van a coincidir con el número total de estados independientes que tengan de energía ese exponente de $q$.
Y, ¿qué ocurre si, además, ese sistema físico tiene como simetría el grupo monstruo? Entonces, el espacio vectorial de todos los estados de ese sistema físico con una energía dada tiene que ser una representación del grupo monstruo. Los exponentes de la expansión en serie de potencias de $q$ de la función de partición del sistema serán, por tanto, ¡las dimensiones de esas representaciones del grupo monstruo!
¿Conocemos algún sistema físico que tenga por simetría el grupo monstruo? Sí. Si cogemos la teoría de cuerdas y la compactificamos en un toro de 24 dimensiones generado a partir de una red especial, denominada Leech lattice, ¡esta teoría física tiene exactamente como simetría el grupo monstruo! Es muy importante que lo que viva en ese toro sean cuerdas. Si fuesen partículas puntuales, la simetría de ese sistema físico sería simplemente la de la red que genera ese toro, que no es el grupo monstruo, sino otro grupo esporádico mucho más pequeño. Pero la magia de la teoría de cuerdas hace que los sistemas físicos tengan simetrías ampliadas, respecto de las que ingenuamente uno esperaría analizando la geometría en la que hacemos que éstas se propaguen.
Ya sólo nos falta, para desvelar el secreto del monstrous moonshine, probar que la función de partición de la cuerda en ese toro sea la función j. Sin entrar en detalles técnicos, podemos comentar aquí que las funciones de partición de los sistemas cuánticos son la continuación analítica de la integral de camino de Feynman, en la que identificamos los estados inicial y final y sumamos para todos ellos. En el caso de una cuerda, esto se corresponde con una sábana de mundo que vuelve sobre sí misma, es decir, una sábana de mundo que tiene la topología de un 2-toro.
La función de partición es, por tanto, una función de la estructura compleja $\tau$ de ese toro, aunque es invariante ante todas las transformaciones modulares. Y en este caso, esta función es precisamente la función j. Si se calculan todos los detalles, se puede ver que el espacio vectorial de todos los estados excitados en el primer nivel forma una representación del grupo monstruo que es suma directa de la representación singlete (trivial), de dimensión 1, y de la representación irreducible más pequeña, de dimensión 196883, y ese es el motivo por el que el coeficiente de $q^1$ está multiplicado por (196883+1). Algo parecido ocurre también con el resto de coeficiente de la expansión de la función j [Borcherds1992], pero mientras que el estudio del grupo monstruo y sus representaciones es muy complicado, los coeficientes de la expansión en serie de potencias de $q$ de la función j son más fáciles de calcular. Este resultado es tan importante que por él le dieron a Richard Borcherds la Medalla Fields en 1998.
Aunque Borcherds en su demostración rigurosa evita mencionar la mayoría de los conceptos físicos que le guiaron, es la teoría de cuerdas la que ha permitido la conexión entre estas dos ramas de la matemáticas: la teoría de representaciones de los grupos esporádicos y la de las transformaciones conformes en el plano complejo. Y el monstruous moonshine no es un ejemplo aislado. Otras compactificaciones de la teoría de cuerdas también explican otras coincidencias de la misma familia que el monstruous moonshine. De hecho, este asunto ha desencadenado una auténtica revolución en matemáticas de donde ha salido toda una rama nueva: el de las álgebras Kac-Moody generalizadas. Las relaciones entre coeficientes de funciones especiales, la teoría de cuerdas y las representaciones de grupos son a día de hoy un campo activo de investigación, llevado a cabo tanto por matemáticos como por físicos teóricos.
¿Dónde está la clave de este éxito de la física teórica en producir estos regalos valiosísimos para los matemáticos? Todos estos ejemplos que acabamos de mencionar nos indican que la clave está en el hecho de que en mecánica cuántica los físicos utilizamos la integral de camino de Feynman para hallar las probabilidades de los distintos resultados de los experimentos y los valores esperados de los observables, y también para calcular las funciones de partición de los sistemas físicos al hacer la continuación analítica hacia la signatura euclídea. Al sumar las amplitudes de probabilidad para todos los caminos, los estamos considerando a todos a la vez dentro del mismo objeto matemático. Para Dijkgraaf, "este enfoque holístico de considerar todo en un sólo paquete está acorde con el espíritu de la matemática moderna, donde el estudio de las categorías de objetos está más enfocado hacia las relaciones mutuas entre objetos que hacia algún ejemplo individual específico. Es esta vista de pájaro de la teoría cuántica la que nos trae estos resultados tan sorprendentes."
Conclusión
Analizar sólo el álgebra y la geometría, y olvidarte de la física, conlleva una versión estrecha de los objetos matemáticos. Aunque la forma que tenemos los físicos de abordar los problemas es considerada todavía por muchos matemáticos como el "lado oscuro" de su disciplina, lo cierto es que ésta les proporcionaría un poder casi ilimitado si no la despreciaran tan habitualmente.
Para poder comprender de verdad los grandes misterios del pensamiento racional, uno debe estudiar todos sus aspectos, no sólo la visión dogmática y limitada de los matemáticos. Cualquier estudiante de matemáticas que aspire a llegar a ser un a pensador completo y sabio debe abarcar un punto de vista más amplio de la matemática, aquel en el que, además de tener presente el significado algebraico y geométrico de los objetos matemáticos, se considere también el significado físico de los mismos. En particular, la teoría de cuerdas es hoy en día una fuente de resultados fascinantes y líneas nuevas de investigación en matemáticas. Nadie puede estar al día acerca del estado actual de la matemática moderna si se empeña en ignorar este hecho.
Hemos empezando este post con la gráfica de una función:
He enseñado esta gráfica durante años a muchas personas mayores que han estudiado matemáticas y les he preguntado si les daba miedo.
—¿por qué habría de asustar la gráfica de una función? Las matemáticas no me dan miedo. Soy matemática— me responden normalmente.
Pero esta gráfica no es la representación de una función matemática que vive en el mundo de las ideas de Platón. El mundo de los objetos matemáticos no existe. Álgebra, geometría y física son la misma cosa. Este dibujo en realidad representa...
|
|
|
|
|
|
|
V
Sigue bajando
|
|
|
|
|
|
|
V
una serpiente boa que digiere un elefante:
Sobre el autor: Sergio Montañez Naz es doctor en física y profesor de secundaria de la enseñanza pública en la Comunidad de Madrid.
Referencias bibliográficas
- Arnold V.I. (1998) "On teaching mathematics". Uspekhi Mat. Nauk 53 (1998), no. 1, 229-234.
- Borcherds, Richard. (1992). "Monstrous moonshine and monstrous Lie superalgebras". Inventiones Mathematicae. 109. 405-444. 10.1007/BF01232032.
- Conway J. H., Norton S. P. (1979), "Monstrous Moonshine", Bulletin of the London Mathematical Society, Volume 11, Issue 3, October 1979, Pages 308–339, https://doi.org/10.1112/blms/11.3.308.
- Dijkgraaf, Robert (2014) "The Unreasonable Effectiveness of Quantum Physics in Modern Mathematics". Lecture given in Perimeter Institute for Theoretical Physics. March 5th, 2014
Mathematics - González Urbaneja P. M. (2003). Los orígenes de la geometría analítica. Materiales de historia de la ciencia Vol. 6, Fundación Canaria Orotava.
- Hori, K., S. Katz, A. Klemm, R. Pandharipande, R. Thomas, C. Vafa, R. Vakil, and E. Zaslow, (2003), Mirror symmetry, American Mathematical Society.
- Witten, E., (1989), “Quantum field theory and the Jones polynomial,” Commun. Math. Phys. 121, 351.



















































No hay comentarios:
Publicar un comentario